補碼

---

二進位制數系統是數字系統中最流行的數製表示技術之一。在二進位制系統中，只有兩個符號或可能的數字值，即 0（關）和 1（開）。由任何只有兩種工作狀態或可能條件的裝置表示。

通常，二進位制數有兩種補碼：一補碼和二補碼。要獲得二進位制數的一補碼，只需反轉給定的數字。例如，二進位制數 110010 的一補碼是 001101。要獲得二進位制數的二補碼，就是給定數字的一補碼加上最低有效位 (LSB) 的 1。例如，二進位制數 10010 的二補碼是 (01101) + 1 = 01110。

二進位制數的二補碼

將二進位制數轉換為二補碼有一個簡單的演算法。要獲得二進位制數的二補碼，只需反轉給定的數字，然後將結果的最低有效位 (LSB) 加 1。下面給出了 4 位二補碼的實現。

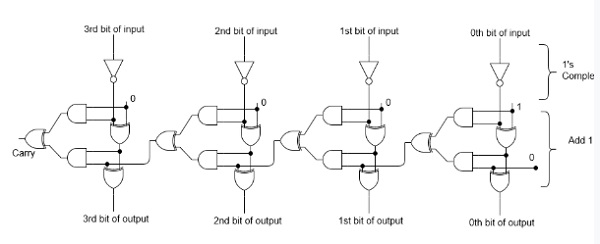
示例 1 - 查詢二進位制數 10101110 的二補碼。

只需反轉給定二進位制數的每一位，結果為 01010001。然後將此結果的 LSB 加 1，即 01010001 + 1 = 01010010，這就是答案。

示例 2 - 查詢二進位制數 10001.001 的二補碼。

只需反轉給定二進位制數的每一位，結果為 01110.110。然後將此結果的 LSB 加 1，即 01110.110 + 1 = 01110.111，這就是答案。

示例 3 - 查詢每個 3 位二進位制數的二補碼。

只需反轉給定二進位制數的每一位，然後將這些反轉後的數字的 LSB 加 1，

二進位制數	一補碼	二補碼
000	000 (+0) 和 111 (-0)	000
001	110	111
010	101	110
011	100	101
100	011	100
101	010	011
110	001	010
111	000	001

二補碼二進位制數的用途

二補碼二進位制數有多種用途，主要用於有符號二進位制數表示和二進位制數的各種算術運算，例如加法、減法等。由於二補碼錶示是明確的，因此它在計算機數表示中非常有用。

有符號二進位制數表示中的二補碼

正數簡單地表示為簡單的二進位制表示。但如果數字為負數，則使用二補碼錶示。首先用正號表示數字，然後取該數字的二補碼。

示例 - 假設我們使用 5 位暫存器。-5 和 +5 的表示如下所示

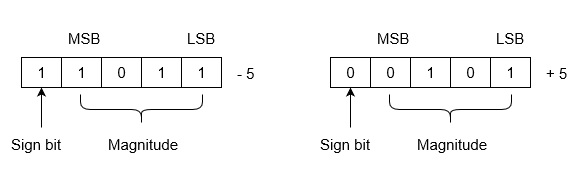
+5 的表示與符號幅值法中的表示相同。-5 使用以下步驟表示

(i) +5 = 0 0101

(ii) 取 0 0101 的二補碼，即 1 1011。MSB 為 1，表示該數為負數。

負數的 MSB 始終為 1。

數字範圍 - 對於 k 位暫存器，可以儲存的最大正數為 (2^(k-1)-1)，可以儲存的最小負數為 -(2^(k-1))。

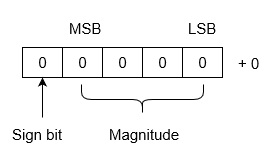
此係統的優點是 0 只有一個表示，即 -0 和 +0。在二補碼錶示中，零 (0) 始終被認為是正數（符號位為 0）。因此，它是一種唯一或明確的表示。

讓我們看看算術運算：二補碼二進位制數的減法和加法。

二補碼減法

使用二補碼進行兩個二進位制數減法的演算法如下所示：

• 取被減數的二補碼
• 與被減數相加
• 如果上述加法的結果有進位位 1，則將其丟棄，此結果將為正數。
• 如果沒有進位位 1，則取結果的二補碼，這將為負數

請注意，被減數是要從另一個數（即被減數）中減去的數。

另請注意，新增“迴圈進位位”僅發生在一補碼算術運算中，而不發生在二補碼算術運算中。

示例（情況 1：當進位位為 1 時） - 計算 10101 - 00101

根據上述演算法，取被減數 00101 的二補碼，結果為 11011，然後將兩者相加。因此，10101 + 11011 = 1 10000。由於存在進位位 1，因此丟棄此進位位 1，並取此結果為 10000，它將為正數。

示例（情況 2：當沒有進位位時） - 計算 11001 - 11100

根據上述演算法，取被減數 11110 的二補碼，結果為 00100。然後將兩者相加，因此，11001 + 00100 = 11101。由於沒有進位位 1，因此取上述結果的二補碼，結果為 00011，這是一個負數，即 00011，這就是答案。

同樣，您可以減去兩個混合（帶小數部分）的二進位制數。

二補碼加法 -

使用二補碼進行兩個二進位制數加法的情況有所不同。這些情況解釋如下。

情況 1 - 當正數的幅度更大時，正數和負數的加法：

當正數的幅度更大時，只需取負數的二補碼，並丟棄進位位 1，此結果將為正數。

示例 - 加上 1110 和 -1101。

因此，取 1101 的二補碼，結果為 0011，然後與給定數字相加。因此，1110 + 0011 = 1 0001，並且進位位 1 被丟棄，此結果將為正數，即 +0001。

請注意，如果暫存器大小較大，則使用 MSB 位的符號擴充套件方法來保留數字的符號。

情況 2 - 當負數的幅度更大時，正數和負數的加法 -

當負數的幅度更大時，取負數的二補碼，並與給定的正數相加。由於不會有任何迴圈進位位，因此取結果的二補碼，此結果將為負數。

示例 - 在五位暫存器中新增 1010 和 -1100。

請注意，有五位暫存器，因此這些新數字將為 01010 和 -01100。現在取 01100 的二補碼，結果為 10100，並新增 01010 + 10100 = 11110。然後取此結果的二補碼，結果為 00010，這是一個負數，即 -00010，這就是答案。

情況 3 - 兩個負數的加法 -

您需要對這兩個數字取二補碼，然後將這兩個數字的二補碼相加。由於始終存在迴圈進位位，因此將其丟棄。現在，也取先前結果的二補碼，因此這將為負數。

或者，您可以將這兩個二進位制數相加，並取結果，該結果將僅為負數。

示例 - 在五位暫存器中新增 -1010 和 -0101。

這五個位數字為 -01010 和 -00101。新增這些數字的二補碼，10110 + 11011 = 1 10001。由於存在進位位 1，因此將其丟棄。現在取此結果的二補碼，結果為 01111，這是一個負數，即 -01111，這就是答案。

請注意，由於不存在“迴圈進位位”的加法，因此二補碼算術運算比一補碼算術運算容易得多。