一階系統暫態響應
為了理解一階系統的暫態響應,考慮一個具有單位負反饋的閉環系統的框圖。

具有單位負反饋的系統的開環增益G(s)由下式給出:
$$G(s)=\frac{1}{s\tau}$$
具有單位負反饋的系統的閉環傳遞函式為:
$$\frac{C(s)}{R(s)}=\frac{G(s)}{1+G(s)}=\frac{1}{s\tau+1}\:\:\:...(1)$$
其中:
R(s) = 輸入訊號r(t)的拉普拉斯變換,
C(s) = 輸出訊號c(t)的拉普拉斯變換,
τ = 系統的時間常數。
我們可以看到,閉環傳遞方程的分母項中s的冪為1。因此,該系統被稱為一階系統。
$$C(s)=\frac{1}{s\tau+1}R(s)\:\:\:...(2)$$
一階系統的單位階躍響應
將單位階躍訊號作為輸入應用於一階系統:
$$r(t)=u(t)$$
對兩邊進行拉普拉斯變換:
$$R(s)=\frac{1}{s}$$
$$C(s)=(\frac{1}{s\tau+1})(\frac{1}{s})=\frac{1}{s(s\tau+1)}\:\:\:....(3)$$
透過對方程(3)進行部分分式分解,我們得到:
$$\frac{1}{s(s\tau+1)}=\frac{A}{s}+\frac{B}{(s\tau+1)}=\frac{A(s\tau+1)+Bs}{s(s\tau+1)}\:\:\:\:...(4)$$
比較方程(4)的左右兩邊,我們得到:
$$A(s\tau+1)+Bs=1\:\:\:...(5)$$
透過對方程(5)兩邊的常數項進行比較,我們得到A = 1。將A = 1代入方程(5),我們有:
$$B+\tau=0\Rightarrow\:B=-\tau$$
現在,將A和B的值代入方程(4),我們得到:
$$C(s)=\frac{1}{s}-\frac{\tau}{s\tau+1}=\frac{1}{s}-\frac{1}{s+\frac{1}{\tau}}\:\:\:...(6)$$
對方程(6)兩邊進行拉普拉斯逆變換:
$$C(t)=(1-e^{\frac{-t}{\tau}})u(t)\:\:\:...(7)$$

方程(7)表示一階系統對單位階躍輸入的響應,它既有穩態項也有暫態項。當t = 0時,單位階躍響應c(t)的值為零。對於t的所有正值,它將從零逐漸增加到穩態值一。
一階系統的單位斜坡響應
在一階系統的輸入端使用單位斜坡訊號。
$$\because\:\:r(t)=t\:u(t)$$
進行拉普拉斯變換:
$$R(s)=\frac{1}{s^{2}}$$
由於一階系統的響應由下式給出:
$$C(s)=(\frac{1}{s\tau+1})R(s)\:\:\:\:...(8)$$
將R(s)的值代入方程(8),我們有:
$$C(s)=(\frac{1}{s\tau+1})(\frac{1}{s^{2}})\:\:\:\:...(9)$$
透過進行部分分式分解求解,我們得到:
$$C(s)=\frac{1}{s^{2}}-\frac{\tau}{s}+\frac{\tau}{s+\frac{1}{\tau}}\:\:\:...(10)$$
對方程(10)進行拉普拉斯逆變換,我們有:
$$C(t)=(t-\tau+\tau\:e^{-t/\tau})u(t)\:\:\:\:for\:t\geq0\:\:\:...(11)$$
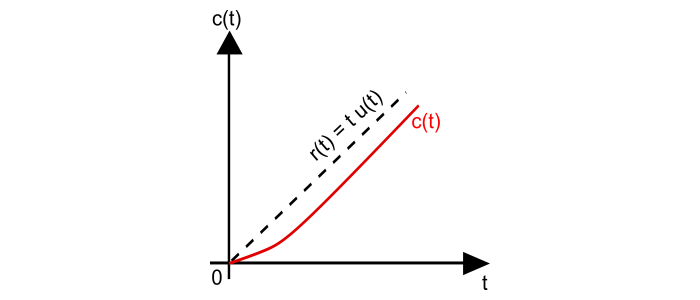
方程(11)顯示了一階系統對單位斜坡輸入的時間響應,對於t的所有正值,c(t)都遵循單位斜坡訊號。但是,與輸入訊號存在τ個單位的偏差。從方程(t)中也可以看出,c(t)既有穩態項也有暫態項。
一階系統的脈衝響應
在一階系統的輸入端施加單位脈衝響應:
$$r(t)=\delta(t)$$
對兩邊進行拉普拉斯變換:
$$R(s)=1$$
由於一階系統的響應為:
$$C(s)=(\frac{1}{s\tau+1})R(s)\:\:\:\:...(12)$$
將R(s) = 1代入方程(12),我們有
$$C(s)=(\frac{1}{s\tau+1})(1)=(\frac{1}{s\tau+1})$$
$$C(s)=\frac{1}{\tau(s+1/\tau)}=\frac{1}{\tau}(\frac{1}{s+1/\tau})\:\:\:\:...(13)$$
對方程(13)兩邊進行拉普拉斯逆變換,我們得到:
$$C(t)=\frac{1}{\tau}e^{(-t/\tau)}u(t)\:\:\:\:for\:t\geq0\:\:\:\:...(14)$$
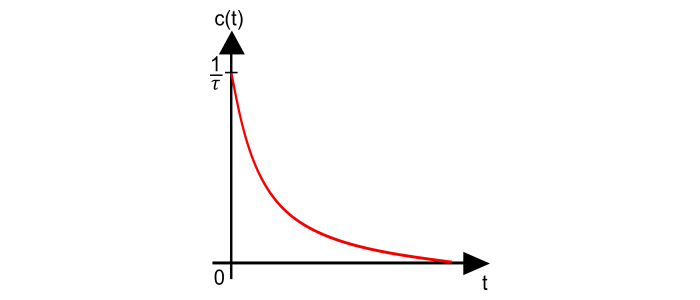
方程(14)顯示了一階系統的單位脈衝響應。對於t的正值,c(t)是一個指數衰減訊號。
一階系統時間響應總結
| 輸入 | 輸出 |
|---|---|
| 單位階躍訊號 $r(t)=u(t)\:\:\:For,t\geq0$ | $$c(t)=(1-e^{-t/\tau})u(t)\:\:\:For,t\geq0$$ |
| 單位斜坡訊號 $r(t)=t\:u(t)\:\:\:For,t\geq0$ | $$c(t)=(t-\tau+\tau\:e^{-t/\tau})u(t)\:\:\:For,t\geq0$$ |
| 單位脈衝訊號 $r(t)=\delta(t)\:\:\:For,t\geq0$ | $$c(t)=\frac{1}{\tau}e^{-t/\tau}u(t)\:\:\:For,t\geq0$$ |


 資料結構
資料結構 網路
網路 關係資料庫管理系統 (RDBMS)
關係資料庫管理系統 (RDBMS) 作業系統
作業系統 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C語言程式設計
C語言程式設計 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP