資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究解釋 DFA 中的補集過程
下面解釋了確定性有限自動機 (DFA) 中的補集過程。
讓我們以一個由 (Q, Σ, δ,q0,F) 定義的 DFA 為例，它接受語言 L1。現在，接受語言 L2 的 DFA，其中 L2 = ̅L1，定義如下：
(Q, Σ, δ,q0,Q-F)
DFA 的補集是透過將非終結狀態設為終結狀態，並將終結狀態設為非終結狀態得到的。
被補集 DFA L2 接受的語言是語言 L1 的補集。
示例
讓我們考慮一些示例，以清楚地瞭解 DFA 的補集過程。
示例 1
考慮兩種語言 L1 和 L2。
在 L1 中，所有字串在字母表 {a,b} 上以 'a' 開頭
L1={a,ab,aa,aba,aab,aaa,……}
在 L2 中，所有字串在字母表 {a,b} 上不以 'a' 開頭
L2={€, b,ba,bab,baa,bba,……}
在這裡，我們可以觀察到這兩種語言的形式為：
L2 = ̅L1
下面給出了接受所有以 'a' 開頭的 {a, b} 上的字串集的 L1 的 DFA 的狀態轉換圖：
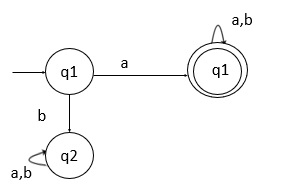
q0 在 'a' 上轉到 q1，q1 是一個終結狀態，並生成以字母 'a' 開頭的字串
{a,ab,aab,abb,aaab,……}
其中 q2 是死狀態。
構建補集的 DFA
現在，我們可以透過簡單地交換終結狀態和非終結狀態來構建補集的 DFA。
這指的是將非終結狀態更改為終結狀態，並將終結狀態更改為非終結狀態。
構建補集的 DFA 後的狀態轉換圖如下：
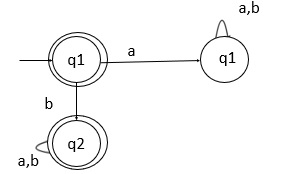
以上狀態轉換圖是補集 DFA，它接受不以 'a' 開頭的字串。
q0 在 'a' 上轉到 q1，q1 是一個死狀態，因此，可以清楚地看到以上狀態轉換 DFA 不會生成以 'a' 開頭的字串。
更新於: 2021 年 6 月 15 日
1K+ 次檢視
廣告