Java 資料結構與演算法 - 佇列

概述

佇列是一種類似於棧的資料結構，主要區別在於第一個插入的元素也是第一個被移除的元素（FIFO - 先進先出），而棧則是基於後進先出（LIFO）的原則。

隊列表示

基本操作

• 插入/入隊 (enqueue) − 將一個元素新增到佇列的尾部。

• 移除/出隊 (dequeue) − 從佇列的頭部移除一個元素。

在本文中，我們將使用陣列來實現佇列。佇列還支援一些其他的操作，如下所示。

• 檢視 (peek) − 獲取佇列頭部元素。

• 是否已滿 (isFull) − 檢查佇列是否已滿。

• 是否為空 (isEmpty) − 檢查佇列是否為空。

插入/入隊操作

每當一個元素插入到佇列中時，佇列會增加尾部索引以供後續使用，並將該元素儲存在儲存區的尾部。如果尾部到達最後一個索引，它會環繞到最底部位置。這種安排稱為環繞，這樣的佇列稱為迴圈佇列。此方法也稱為入隊操作。

public void insert(int data){
   if(!isFull()){
      if(rear == MAX-1){
         rear = -1;            
      }       
      
      intArray[++rear] = data;
      itemCount++;
   }
}

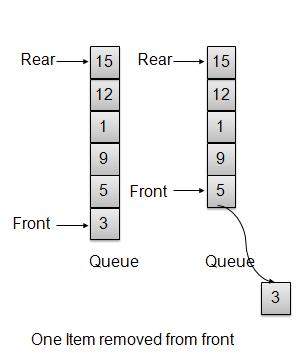
移除/出隊操作

每當需要從佇列中移除一個元素時，佇列會使用頭部索引獲取該元素並增加頭部索引。作為環繞安排，如果頭部索引大於陣列的最大索引，則將其設定為 0。

 	 	
public int remove(){
   int data = intArray[front++];
   if(front == MAX){
      front = 0;
   }
   itemCount--;
   return data;  
}

佇列實現

Queue.java

package com.tutorialspoint.datastructure;

public class Queue {
    
   private final int MAX;
   private int[] intArray;
   private int front;
   private int rear;
   private int itemCount;

   public Queue(int size){
      MAX = size;
      intArray = new int[MAX];
      front = 0;
      rear = -1;
      itemCount = 0;
   }

   public void insert(int data){
      if(!isFull()){
         if(rear == MAX-1){
            rear = -1;            
         }       

         intArray[++rear] = data;
         itemCount++;
      }
   }

   public int remove(){
      int data = intArray[front++];
      if(front == MAX){
         front = 0;
      }
      itemCount--;
      return data;  
   }

   public int peek(){
      return intArray[front];
   }

   public boolean isEmpty(){
      return itemCount == 0;
   }

   public boolean isFull(){
      return itemCount == MAX;
   }

   public int size(){
      return itemCount;
   }    
}

演示程式

QueueDemo.java

package com.tutorialspoint.datastructure;

public class QueueDemo {
   public static void main(String[] args){
      Queue queue = new Queue(6);
      
      //insert 5 items
      queue.insert(3);
      queue.insert(5);
      queue.insert(9);
      queue.insert(1);
      queue.insert(12);

      // front : 0
      // rear  : 4
      // ------------------
      // index : 0 1 2 3 4 
      // ------------------
      // queue : 3 5 9 1 12

      queue.insert(15);

      // front : 0
      // rear  : 5
      // ---------------------
      // index : 0 1 2 3 4  5 
      // ---------------------
      // queue : 3 5 9 1 12 15

      if(queue.isFull()){
         System.out.println("Queue is full!");   
      }


      //remove one item
      int num = queue.remove();
      System.out.println("Element removed: "+num);
      // front : 1
      // rear  : 5
      // -------------------
      // index : 1 2 3 4  5
      // -------------------
      // queue : 5 9 1 12 15

      //insert more items
      queue.insert(16);

      // front : 1
      // rear  : -1
      // ----------------------
      // index : 0  1 2 3 4  5
      // ----------------------
      // queue : 16 5 9 1 12 15

      //As queue is full, elements will not be inserted.
      queue.insert(17);
      queue.insert(18);
 
      // ----------------------
      // index : 0  1 2 3 4  5
      // ----------------------
      // queue : 16 5 9 1 12 15
      System.out.println("Element at front: "+queue.peek());

      System.out.println("----------------------");
      System.out.println("index : 5 4 3 2  1  0");
      System.out.println("----------------------");
      System.out.print("Queue:  ");
      while(!queue.isEmpty()){
         int n = queue.remove();            
         System.out.print(n +" ");
      }
   }
}

如果我們編譯並執行上述程式，則會產生以下結果：

Queue is full!
Element removed: 3
Element at front: 5
----------------------
index : 5 4 3 2  1  0
----------------------
Queue:  5 9 1 12 15 16