資料結構
網路
關係型資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究設計一個識別至少包含兩個 0 和至少包含兩個 1 的字串的 DFA
確定性有限自動機 (DFA) 是一個 5 元組
M=(Q, Σ, δ,q0,F)
其中，
- Q：稱為狀態的有限集合。
- Σ：稱為字母表的有限集合。
- δ：Q × Σ → Q 是轉移函式。
- q0 ϵ Q 是起始狀態或初始狀態。
- F：終止狀態或接受狀態。
問題
構造一個識別至少包含兩個 0 和至少包含兩個 1 的字串的 DFA。
解決方案
基於給定條件在字母表 Σ ={0,1} 上生成的語言是 -
L={0011,001011,0001010,0011001,010101,……}
給定的語言接受至少兩個 0，意味著它可以接受兩個或兩個以上的 0，並且至少兩個 1，意味著它接受兩個或兩個以上的 1。
假設，
- 輸入 - 00010
- 輸出 - 字串被拒絕
因為，給定的輸入不包含至少兩個 1。
即使它至少包含兩個 0，它也不會接受該字串。
為了接受字串，兩個條件都必須滿足，如果其中一個不滿足，則該字串將不會被機器接受。
- 輸入 - 001001001
- 輸出 - 字串被接受
現在為給定的輸入構造 DFA -
| 狀態 | 0 的數量 | 1 的數量 |
|---|---|---|
| → q0 | 0 | 0 |
| q1 | 0 | 1 |
| q2 | 0 | > =2 |
| q3 | 1 | 0 |
| q4 | 1 | 1 |
| q5 | 1 | > =2 |
| q6 | > =2 | 0 |
| q7 | > =2 | 1 |
| *q8 | > =2 | > =2 |
DFA 將如下所示 -
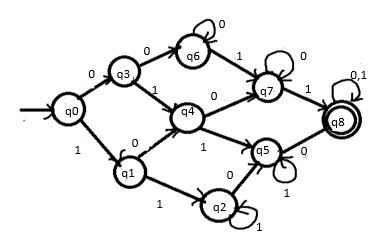
解釋
如果輸入是 1，則 1 的數量增加到 1。轉移到狀態 q1。如果輸入是 0，則 0 的數量增加到 1。轉移到狀態 q3。
如果輸入是 1，則 1 的數量增加到 2。轉移到狀態 q2。如果輸入是 0，則 0 的數量增加到 1。轉移到狀態 q4。
如果輸入是 1，則 1 的數量始終增加 1。然後保持在同一狀態。如果輸入是 0，則 0 的數量增加到 1。轉移到狀態 q5。
如果輸入是 1，則 1 的數量增加到 1。轉移到狀態 q4。如果輸入是 0，則 0 的數量增加到 2。轉移到狀態 q6。
如果輸入是 1，則 1 的數量增加到 2。轉移到狀態 q5。如果輸入是 0，則 0 的數量增加到 2。轉移到狀態 q7。
如果輸入是 1，則 1 的數量始終增加 1。然後保持在同一狀態。如果輸入是 0，則 0 的數量增加到 2。轉移到狀態 q8
如果輸入是 1，則 1 的數量增加到 1。轉移到狀態 q7。如果輸入是 0，則 0 的數量持續增加 1。然後保持在同一狀態。
如果輸入是 1，則 1 的數量增加到 2。轉移到狀態 q8。如果輸入是 0，則 0 的數量持續增加 1。然後保持在同一狀態。
如果輸入是 1，則 1 的數量始終增加 1。然後保持在同一狀態。如果輸入是 0，則 0 的數量持續增加 1。然後保持在同一狀態。
最後，如果字串結束，則它被接受。
3K+ 瀏覽量
