資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究構建交替出現 0 和 1 的 DFA
問題
構建一個確定性有限自動機 (DFA)，其語言由在字母表 ∑ ={0,1} 上交替出現 0 和 1 的字串組成。
解決方案
If Σ = {0, 1}
(ε + 1)(01)*
(ε + 0) is the set of strings that alternate 0’s and 1’s
Another expression for the same language is (01)*+ 1(01)*+ (01)*0+ 1(01)*0.給定語言生成的字串如下所示：
如果沒有輸入是 0 或 1，則它生成 {ε}。
字串以 0 開頭，後跟 1 = {0101…}。
字串以 1 開頭，後跟 0 ={101010….. }
因此，根據字串生成，可以清楚地看出字串以 ε、(01)*、(10)* 開頭，但沒有限制字串只能以 0 或 1 開頭，因此考慮到所有這些點，滿足給定語言中交替出現 0 和 1 的表示式為：
(01)* + (10)* + 0(10)* + 1(01)*
DFA
給定語言的 DFA 為：
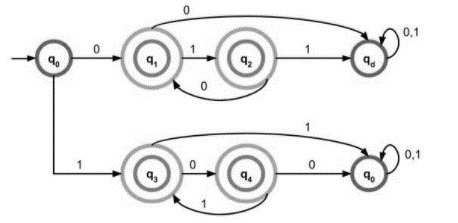
解釋
從初始狀態開始，它生成的字串，q0 上的 0 轉到 q1，它是最終狀態之一，只接受 0，滿足給定條件。
從初始狀態開始，它生成的字串，q0 上的 1 轉到 q3，它是最終狀態之一，只接受 1，滿足給定條件。
q0 達到最終狀態 q2，它生成字串“01”，該字串被語言接受。
q0 達到最終狀態之一 q4，它生成字串“10”，該字串被語言接受。
類似地，DFA 也接受其餘字串。
更新於： 2021年6月15日
3K+ 瀏覽量
廣告