資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會研究
服裝研究
法學研究JavaScript中的深度優先搜尋遍歷
DFS 首先訪問子節點，然後再訪問兄弟節點；也就是說，它在探索廣度之前會遍歷任何特定路徑的深度。在實現該演算法時，通常使用堆疊（通常是程式的呼叫堆疊，透過遞迴）。
以下是 DFS 的工作方式：
- 訪問相鄰的未訪問頂點。將其標記為已訪問。顯示它。將其壓入堆疊。
- 如果沒有找到相鄰頂點，則從堆疊中彈出頂點。（它將彈出堆疊中所有沒有相鄰頂點的頂點。）
- 重複規則 1 和規則 2，直到堆疊為空。
讓我們來看一個 DFS 遍歷如何工作的示例。
| 步驟 | 遍歷 | 描述 |
|---|---|---|
| 1 | 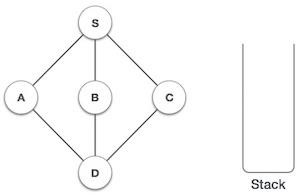 | 初始化堆疊。 |
| 2 | 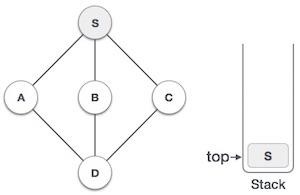 | 將S標記為已訪問，並將其放入堆疊中。從S探索任何未訪問的相鄰節點。我們有三個節點，我們可以選擇任何一個。在本例中，我們將按字母順序選擇節點。 |
| 3 | 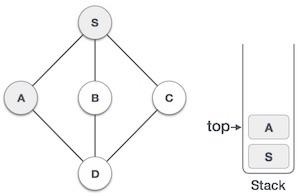 | 將A標記為已訪問，並將其放入堆疊中。從A探索任何未訪問的相鄰節點。S和D都與A相鄰，但我們只關注未訪問的節點。 |
| 4 | 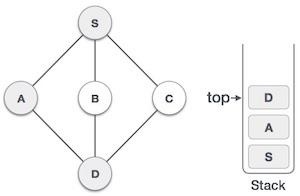 | 訪問D，將其標記為已訪問，並將其放入堆疊中。這裡，我們有B和C節點，它們與D相鄰，並且都未訪問。但是，我們將再次按字母順序選擇。 |
| 5 | 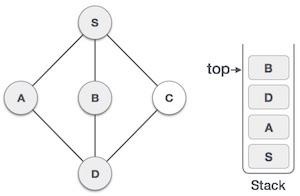 | 我們選擇B，將其標記為已訪問，並將其放入堆疊中。這裡B沒有任何未訪問的相鄰節點。因此，我們將B從堆疊中彈出。 |
| 6 | 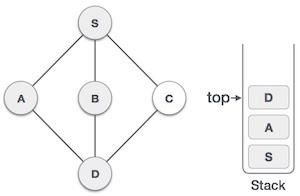 | 我們檢查堆疊頂部是否返回到上一個節點，並檢查它是否有任何未訪問的節點。在這裡，我們發現D位於堆疊頂部。 |
| 7 | 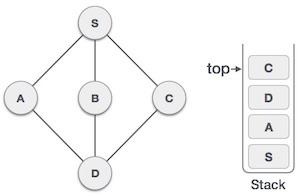 | 現在，D唯一未訪問的相鄰節點是C。因此，我們訪問C，將其標記為已訪問，並將其放入堆疊中。 |
由於C沒有任何未訪問的相鄰節點，因此我們繼續彈出堆疊，直到找到一個具有未訪問相鄰節點的節點。在本例中，沒有這樣的節點，我們繼續彈出堆疊直到堆疊為空。讓我們看看如何在 JavaScript 中實現它。
示例
DFS(node) {
// Create a Stack and add our initial node in it
let s = new Stack(this.nodes.length);
let explored = new Set();
s.push(node);
// Mark the first node as explored
explored.add(node);
// We'll continue till our Stack gets empty
while (!s.isEmpty()) {
let t = s.pop();
// Log every element that comes out of the Stack
console.log(t);
// 1. In the edges object, we search for nodes this node is directly connected to.
// 2. We filter out the nodes that have already been explored.
// 3. Then we mark each unexplored node as explored and push it to the Stack.
this.edges[t]
.filter(n => !explored.has(n))
.forEach(n => {
explored.add(n);
s.push(n);
});
}
}好吧，這很容易。我們實際上只是將佇列換成了堆疊，瞧，我們有了 DFS。這確實是兩者之間唯一的區別。DFS 也可以使用遞迴來實現。但在這種情況下最好避免，因為更大的圖意味著我們需要額外的記憶體來跟蹤呼叫堆疊。
您可以使用以下方法進行測試：
let g = new Graph();
g.addNode("A");
g.addNode("B");
g.addNode("C");
g.addNode("D");
g.addNode("E");
g.addNode("F");
g.addNode("G");
g.addEdge("A", "C");
g.addEdge("A", "B");
g.addEdge("A", "D");
g.addEdge("D", "E");
g.addEdge("E", "F");
g.addEdge("B", "G");
g.DFS("A");輸出
這將給出輸出。
A D E F B G C
更新於：2020年6月15日
4K+ 次瀏覽
廣告