資料結構
網路
RDBMS
作業系統
Java
MS Excel
iOS
HTML
CSS
安卓
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究圖的深度優先搜尋或 DFS
深度優先搜尋 (DFS) 是一種圖遍歷演算法。在這個演算法中，指定了一個起始頂點，當找到相鄰頂點時，它會首先移動到該相鄰頂點，並嘗試以相同的方式遍歷。
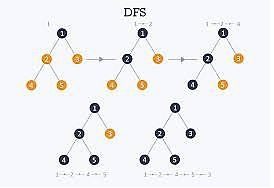
它儘可能遍歷整個深度，然後回溯到以前的頂點以找到新路徑。
為了使用迭代方式實現 DFS，我們需要使用棧資料結構。如果我們想要以遞迴的方式進行，則不需要外部棧，它可以對遞迴呼叫使用內部棧。
輸入：圖的鄰接矩陣。
A B C D E F A 0 1 1 1 0 0 B 1 0 0 1 1 0 C 1 0 0 1 0 1 D 1 1 1 0 1 1 E 0 1 0 1 0 1 F 0 0 1 1 1 0
輸出：DFS 遍歷：C F E B D A
演算法
dfs(頂點，開始)
輸入 - 所有頂點的列表和開始節點。
輸出 - 遍歷圖中的所有節點。
Begin initially make the state to unvisited for all nodes push start into the stack while stack is not empty, do pop element from stack and set to u display the node u if u is not visited, then mark u as visited for all nodes i connected to u, do if ith vertex is unvisited, then push ith vertex into the stack mark ith vertex as visited done done End
示例
#include<iostream>
#include<stack>
using namespace std;
#define NODE 6
typedef struct node{
int val;
int state; //status
}node;
int graph[NODE][NODE] = {
{0, 1, 1, 1, 0, 0},
{1, 0, 0, 1, 1, 0},
{1, 0, 0, 1, 0, 1},
{1, 1, 1, 0, 1, 1},
{0, 1, 0, 1, 0, 1},
{0, 0, 1, 1, 1, 0}
};
void dfs(node *vertex, node start){
node u;
stack<node> myStack;
for(int i = 0; i<NODE; i++){
vertex[i].state = 0;//not visited
}
myStack.push(start);
while(!myStack.empty()){
//pop and print node
u = myStack.top();
myStack.pop();
cout << char(u.val+'A') << " ";
if(u.state != 1){
//update vertex status to visited
u.state = 1;
vertex[u.val].state = 1;
for(int i = 0; i<NODE; i++){
if(graph[i][u.val]){
if(vertex[i].state == 0){
myStack.push(vertex[i]);
vertex[i].state = 1;
}
}
}
}
}
}
int main(){
node vertices[NODE];
node start;
char s;
for(int i = 0; i<NODE; i++){
vertices[i].val = i;
}
s = 'C';//starting vertex C
start.val = s-'A';
cout << "DFS Traversal: ";
dfs(vertices, start);
cout << endl;
}輸出
DFS Traversal: C F E B D A
更新於： 05-Aug-2019
908 次瀏覽
廣告