其他分類方法

在這裡，我們將討論其他分類方法，例如遺傳演算法、粗糙集方法和模糊集方法。

遺傳演算法

遺傳演算法的思想源於自然進化。在遺傳演算法中，首先建立初始種群。這個初始種群由隨機生成的規則組成。我們可以用一個位元串來表示每個規則。

例如，在一個給定的訓練集中，樣本由兩個布林屬性（例如A1和A2）描述。這個給定的訓練集包含兩個類別，例如C1和C2。

我們可以將規則**如果A1並且非A2則C2**編碼成位元串**100**。在這個位元表示中，最左邊的兩位分別代表屬性A1和A2。

同樣，規則**如果非A1並且非A2則C1**可以編碼為**001**。

**注意** - 如果屬性有K個值，其中K>2，那麼我們可以使用K位來編碼屬性值。類別也以相同的方式編碼。

要點 -

• 基於適者生存的概念，形成一個新的種群，該種群由當前種群中最適合的規則及其後代值組成。

• 規則的適應度由其在訓練樣本集上的分類準確性來評估。

• 應用交叉和變異等遺傳運算元來建立後代。

• 在交叉中，交換一對規則的子串以形成一對新的規則。

• 在變異中，規則字串中隨機選擇的位被反轉。

粗糙集方法

我們可以使用粗糙集方法來發現不精確和噪聲資料中的結構關係。

**注意** - 此方法只能應用於離散值屬性。因此，連續值屬性必須在使用前進行離散化。

粗糙集理論基於在給定的訓練資料中建立等價類。構成等價類的元組是不可區分的。這意味著樣本在描述資料的屬性方面是相同的。

在給定的現實世界資料中，有一些類別在可用屬性方面無法區分。我們可以使用粗糙集來**粗略地**定義這些類別。

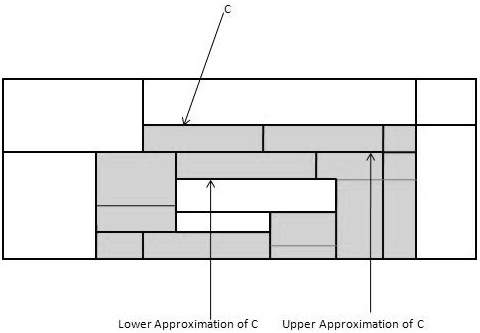
對於給定的類別C，粗糙集定義由以下兩個集合近似 -

• **C的下近似** - C的下近似包含所有根據屬性知識肯定屬於類別C的資料元組。

• **C的上近似** - C的上近似包含所有根據屬性知識不能描述為不屬於C的元組。

下圖顯示了類別C的上近似和下近似 -

模糊集方法

模糊集理論也稱為可能性理論。該理論由Lotfi Zadeh於1965年提出，作為**二值邏輯**和**機率論**的替代方案。該理論允許我們在較高的抽象級別上工作。它還為我們處理資料的不精確測量提供了手段。

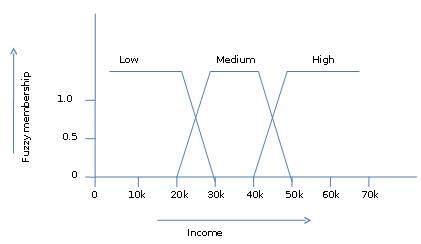
模糊集理論還允許我們處理模糊或不精確的事實。例如，成為高收入人群的成員是不精確的（例如，如果50,000美元是高的，那麼49,000美元和48,000美元呢）。與傳統Crisp集合不同，Crisp集合中的元素要麼屬於S，要麼屬於其補集，但在模糊集理論中，元素可以屬於多個模糊集。

例如，收入值49,000美元屬於中等和高收入模糊集，但程度不同。此收入值的模糊集表示如下：

mmedium_income($49k)=0.15 and mhigh_income($49k)=0.96

其中“m”是分別作用於中等收入和高收入模糊集的隸屬函式。此表示可以圖解如下：