資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究C++ 中圓上等距點之間鈍角的數量
給定一個圓，其圓周上有 K 個等距點。還給定兩個點 A 和 B。目標是計算使用這些點可以形成的三角形的數量，使得它們在內部有一個鈍角 ACB（大於 90o 的角）。點 A 和 B 使得 A < B。
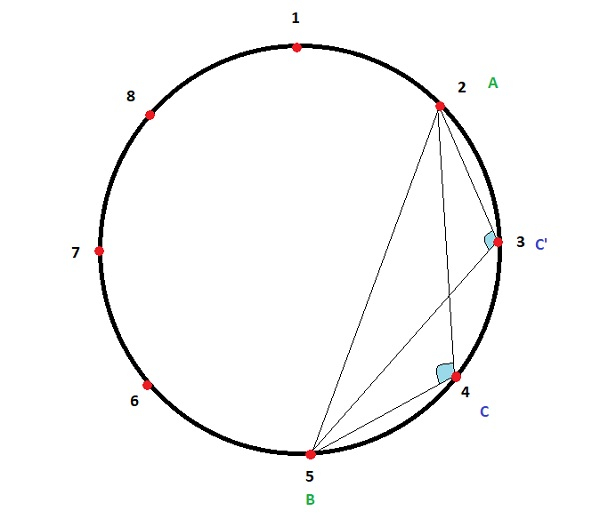
這裡 K=8，A=2，B=5，點的數量=2（C，C'），使得角 LACB，LAC'B 為鈍角。
讓我們透過示例來理解
輸入 − k=10，A=2，B=4
輸出 − 圓上兩個給定點之間等距點的鈍角數量為 - 1
解釋 − 該點將為 C=3
輸入 − k=12，A=2，B=10
輸出 − 圓上兩個給定點之間等距點的鈍角數量為 - 3
下面程式中使用的演算法如下
可以看出，如果 A 和 B 之間的弧越小，則點將只位於該弧上。
計算兩個弧，如果它們長度相等，則沒有這樣的三角形，返回 0。否則將計數設定為較小的弧，即以點數表示的距離。
將輸入作為整數 k、point_a 和 point_b。
函式 Obtuse_angle_circle(int point_a, int point_b, int k) 獲取所有變數並返回圓上兩個給定點之間等距點的鈍角數量
將初始計數設定為 0。
計算第一個弧為 arc_1 = (point_b - point_a) - 1。（b>a）
計算第二個弧為 (k - point_b) + (point_a - 1)。
如果兩個弧相等，則返回 0，因為沒有這樣的點。
如果它們不相等，則將計數更新為兩者中的最小值，因為所有點都位於它上面。
返回計數作為結果。
示例
#include <bits/stdc++.h>
using namespace std;
int Obtuse_angle_circle(int point_a, int point_b, int k){
int count = 0;
int arc_1 = (point_b - point_a) - 1;
int arc_2 = (k - point_b) + (point_a - 1);
if (arc_1 == arc_2){
return 0;
}
count = min(arc_1, arc_2);
return count;
}
int main(){
int k = 10;
int point_a= 1;
int point_b = 4;
cout<<"Count of obtuse angles in a circle with ‘k' equidistant points between 2 given pointsare: "<<Obtuse_angle_circle(point_a, point_b, k);
return 0;
}輸出
如果我們執行以上程式碼，它將生成以下輸出：
Count of obtuse angles in a circle with ‘k' equidistant points between 2 given points are: 2
更新於： 2020-12-03
106 次檢視
廣告