Python程式：根據極角排序笛卡爾點集

假設我們有一個名為points的列表，其中包含一組笛卡爾點。我們需要根據它們的極角對它們進行排序。極角的範圍在0到2*PI之間。如果一些點的極角相同，則根據該點到原點的距離對其進行排列。

因此，如果輸入類似於points = [(1,1), (1,-2),(-2,2),(5,4),(4,5),(2,3),(-3,4)]，

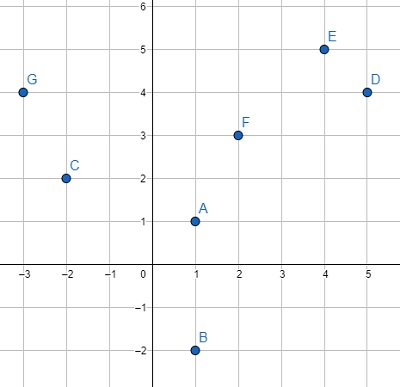
則輸出將為[(5, 4), (1, 1), (4, 5), (2, 3), (-3, 4), (-2, 2), (1, -2)]

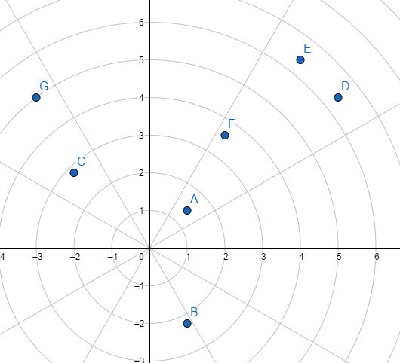
為了解決這個問題，我們將遵循以下步驟：

• 定義一個比較函式key()。它將接收x
• atan := x[1]/x[0] 的反正切
• 如果atan >= 0，則返回(atan, x[1]^2+x[0]^2)，否則返回(2*pi + atan, x[0]^2+x[1]^2)
• 然後使用比較函式key()對points進行排序

示例

讓我們看看下面的實現來更好地理解：

import math
def solve(points):
   def key(x):
      atan = math.atan2(x[1], x[0])
      return (atan, x[1]**2+x[0]**2) if atan >= 0 else (2*math.pi + atan, x[0]**2+x[1]**2)

   return sorted(points, key=key)

points = [(1,1), (1,-2),(-2,2),(5,4),(4,5),(2,3),(-3,4)]
print(solve(points))

輸入

[(1,1), (1,-2),(-2,2),(5,4),(4,5),(2,3),(-3,4)]

輸出

[(5, 4), (1, 1), (4, 5), (2, 3), (-3, 4), (-2, 2), (1, -2)]

Arnab Chakraborty

更新於: 2021年10月11日

1K+ 次檢視

開啟你的 職業生涯

透過完成課程獲得認證

開始學習