餘弦 0

---

引言

cos 0 的值為 1。當直角三角形的角度等於零度時，一個稱為零度角餘弦的數字反映了鄰邊長度與斜邊長度的比率。零度角餘弦的精確值等於 1，零度角的餘弦用六十進位制表示法表示為 cos (0)。

三角函式

數學中的三角函式是將直角三角形的角度與它兩條邊長的比率聯絡起來的實函式。它們也稱為圓函式。

什麼是三角函式

三角函式包括正弦 (sin)、餘弦 (cos)、正切 (tan)、餘切 (cot)、正割 (sec) 和餘割 (csc)，這是用於表示直角三角形邊比率的六個數學函式之一。圖形顯示了這六個三角函式。

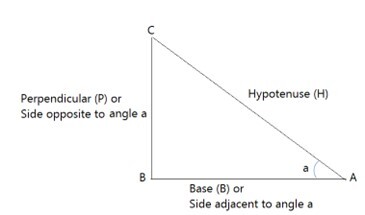
六個基本三角函式

對於一個角，有六個常用的三角函式。它們的名稱和縮寫分別是正弦 (sin)、餘弦 (cos)、正切 (tan)、餘切 (cot)、正割 (sec) 和餘割 (csc)。

• 正弦函式 - 在三角學中，一個角的正弦函式是指直角三角形的對邊（垂直邊）與斜邊的比率。

  正弦函式公式：對邊/斜邊 = CB/CA

• 餘弦函式 - 餘弦（有時縮寫為“cos”）是指斜邊的長度與鄰邊長度的比率。

  餘弦函式公式：鄰邊/斜邊 = AB/CA

• 正切函式 - 正切函式是六個主要三角函式之一，通常表示為 tan x。在直角三角形中，它考慮的是角的對邊和鄰邊的比率。

  正切函式公式：對邊/鄰邊 = CB/BA

• 正割、餘割和餘切函式 - 正割、餘割 (csc) 和餘切是由正弦、餘弦和正切匯出的三個附加函式。餘割 (csc)、正割 (sec) 和餘切 (cot) 分別是正弦、餘弦和正切的倒數。每個函式都有以下公式：

  • sec a = 1/(cos a) = 斜邊/鄰邊 = CA/AB

  • csc a = 1/(sin a) = 斜邊/對邊 = CA/CB

  • cot a = 1/(tan a) = 鄰邊/對邊 = BA/CB

餘弦函式

在三角形中，鄰邊與斜邊的比率稱為餘弦函式（或 cos 函式）。餘弦是三個基本三角函式之一，是正弦的餘角（co-sine）。

餘弦函式的特性

餘弦的特性取決於角所在的象限。餘弦函式是一個獨特的三角函式，具有多種特性。以下是其中一些特性：

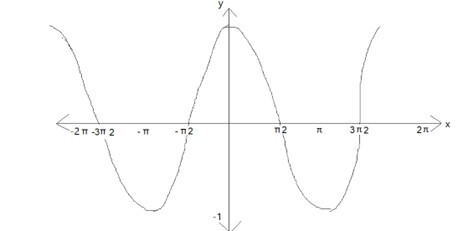
• cos x 圖形在週期為 2π 後重復自身，這表明該函式具有周期 2π 並且是週期性的。

• cos(x) = cos(-x)，使其成為偶函式。

• 所有實數都在餘弦函式的定義域內，其值域為 [-1,1]。

• 餘弦的冪級數展開式為 $\mathrm{cos x =∑_{n=o}^∞(-1)^n \frac{X^{2n}}{(2n)!}}$

餘弦函式恆等式

三角學中有多個涉及餘弦函式的恆等式。利用這些概念可以有效地解決許多數學問題。以下是其中一些：

• cos x = 1/ sec x

• 當 x 在 [-1, 1] 之間時，餘弦函式的反函式為 cos^-1x = arccos x。

• sin²x + cos²x = 1

• cos (x-y) = cos x cos y - sin x sin y

• cos (x+y) = cos x cos y - sin x sin y

• cos 2x = cos² x -sin² x = 2cos² x -1 = 1 - 2sin² x

• 餘弦函式積分：∫cosx=sinx+c，其中 C 為積分常數。

餘弦 0

眾所周知，三角函式是與三角形角度相關的角函式。三角函式已被應用於研究涉及光波和聲波的週期性現象。這些函式對於理解諧波振盪和平均溫度的波動也至關重要。

圓系統中 cos = 0

在圓系統中，“零”不存在。在圓系統中，每個數字都被視為正數。

cos 0 的百分系統

百分系統共有 100 個單位。第一個單位是 1/100，第二個單位是 1/101。這個模式一直保持到 100。

其他角度的餘弦函式

如果已知鄰邊與斜邊的比率，則可以使用反餘弦函式計算任何直角三角形的角度。反餘弦的符號是 cos^-1⁡x 或 arccos。可以使用 cos 函式計算邊長為 1、2 和 3 的直角三角形的角度。

餘弦函式的圖形

三角比也可以看作是變數的函式，該變數是角度的度量。該角度度量可以用度數或弧度表示。在這裡，我們將使用弧度。

例題

1) 求 Sin 45°、Cos 60° 和 Tan 60° 的值。

答案：三角函式表為我們提供：

$$\mathrm{Sin45^\circ =\frac{1}{\sqrt{2}}}$$

$$\mathrm{Cos60^\circ =\frac{1}{2}}$$

$$\mathrm{Tan60^\circ =\sqrt{3}}$$

2) 計算 Sin 105°。

答案：Sin (60° + 45°) 是 sin (105°) 的一種形式，相當於 sin (A + B)。

我們知道 sin 的公式是 sin (A + B) = sin A cos B + cos A sin B

因此，$\mathrm{sin 105^\circ=sin(60^\circ+45^\circ)=sin60^\circ×cos45^\circ+cos60^\circ×sin45^\circ}$

$$\mathrm{=\frac{√3}{2}×\frac{1}{√2}+\frac{1}{2}×\frac{1}{√2}}$$

$$\mathrm{=\frac{√3}{2√2}+\frac{1}{2√2}}$$

$$\mathrm{=\frac{(√3+1)}{2√2}}$$

結論

三角函式是所有三角學的基礎。六個三角函式是 sin、cos、tan、csc、sec 和 cot。三角函式用於幾何中確定直角三角形的未知邊或角。例如，角的對邊和斜邊都相等。為了快速記住公式，可以使用 SOH CAH TOA。

常見問題

1. Cos 0 符號是什麼意思？

0°的餘弦是 1。諸如 cos 0°、30°、45°、60° 和 90° 等常用角度的分數值都可以具有正根。

2. 三角函式表有什麼用？

您可以查閱三角比表，找到各種三角比（包括 0°、30°、45°、60° 和 90°）的標準角的值。

3. 為什麼我們要學習三角學？

使用正弦、餘弦、正切等不同的三角函式分析和簡化方程是三角學最有效和高階的應用。

4. 三角函式有哪些實際應用？

建築和施工、通訊、電氣工程、飛行、GPS、圖形、土地測量、音樂和軌跡都使用或包含三角函式。

5. 什麼是反餘弦？

它是餘弦函式的反函式。有時也縮寫為“arccos”。當已知直角三角形的兩條邊的長度時，它用於計算未知角。