資料結構
網路
關係資料庫管理系統(RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究構造正則語言L = 0(0+1)*1 的 ∈-NFA
在非確定性有限自動機 (NFA) 中，∈ 轉移用於在不使用來自輸入集 Σ 的任何符號的情況下從一個狀態移動到另一個狀態。
∈-NFA 用五元組表示法定義。
{Q, q0, Σ, δ, F}其中：
δ − Q × (Σ∪∈) -> 2Q
Q − 有限狀態集
Σ − 有限輸入符號集
q0 − 初始狀態
F − 終結狀態
δ: 轉移函式
無 ε 轉移的 NFA
NFA 與 DFA 具有相同的五個狀態，但轉移函式不同，如下所示：
$$\delta\colon\:Q\times\:\sum\longrightarrow\:2^{Q}$$
其中：
Q − 有限狀態集
Σ − 有限輸入符號集
q0 − 初始狀態
F − 終結狀態
δ − 轉移函式
示例
考慮如下具有 ε 的 NFA：
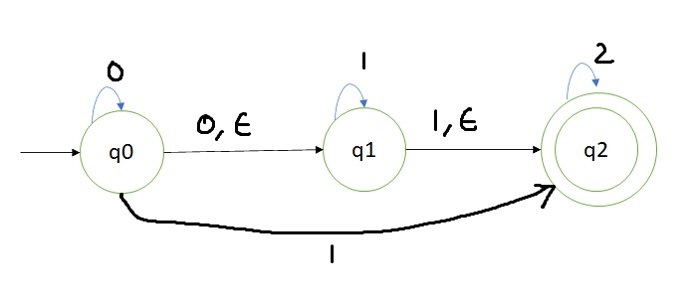
這裡 q0 是一個起始狀態，輸入 0，可以處於狀態 q0 或狀態 q1。
如果我們得到起始符號 1，則透過 epsilon 轉移，我們可以將狀態從 q0 更改為 q1，然後輸入 1 可以處於狀態 q1。
另一方面，從狀態 q0 輸入 1，我們可以到達狀態 q2。
因此，輸入 1 後是否會處於狀態 q1 或 q2 尚不確定。
因此，它被稱為非確定性有限自動機，並且由於有一些 epsilon 移動，我們可以簡單地將狀態從一個狀態更改為另一個狀態。
因此，它被稱為帶有 epsilon 的 NFA。
讓我們考慮給定的語言 L = 0(0+1)*1。
構造 ε-NFA
構造 ε-NFA 的步驟如下：
步驟 1 - 0+ 的帶有 epsilon 的 NFA 如下：
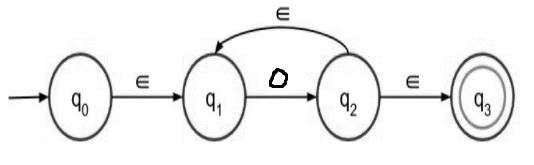
步驟 2 - 0* 的帶有 epsilon 的 NFA 如下：
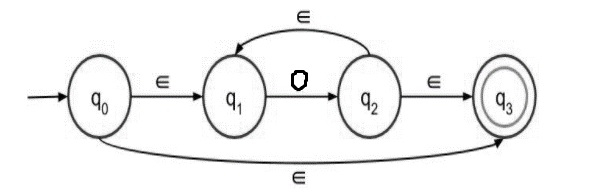
步驟 3 - (0+1) 的帶有 epsilon 的 NFA 如下：
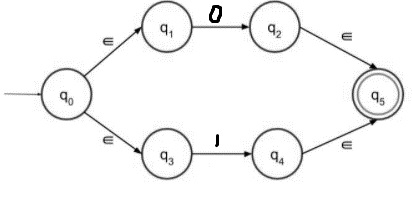
上述狀態轉換圖接受 0 或 1 作為輸入。這兩條路徑都通向最終狀態。
步驟 4 - 01 的帶有 epsilon 的 NFA 如下：
對於串聯，0 必須後跟 1。
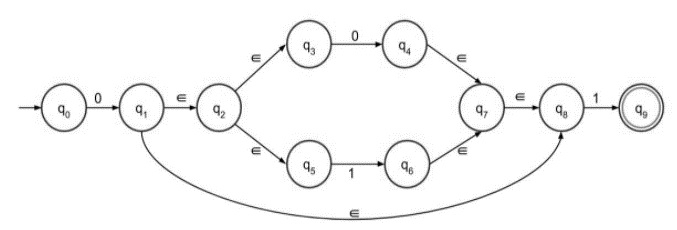
步驟 5 - L = 0(0+1)*1 的 ε-NFA 如下：
L = 0(0+1)*1 分為三部分：0、(0+1)* 和 1。第二部分 (0+1)* 如上所述構造，只需與 0 和 1 串聯，然後遵循第二個規則 0*。
最終帶有 epsilon 移動的 NFA 如下：
8K+ 次瀏覽
