構造一個用於語言 L = {0n1m2m3n | n≥1, m≥1} 的下推自動機 (PDA)。

下推自動機 (PDA) 可以形式化地描述為七元組

(Q, Σ, S, δ, q0, I, F)

其中，

  • Q 是有限數量的狀態
  • Σ 是輸入字母表
  • S 是棧符號
  • Δ 是轉移函式：Q × (Σ ∪ {e}) × S → Q × S*
  • q0 是初始狀態 (q0 ∈ Q)
  • I 是初始棧頂符號
  • F 是接受狀態集 (F ⊆ Q)

問題

構造一個用於語言 0n1m2m3n (其中 n, m ≥ 1) 的 PDA。

解答

因此，由給定語言生成的字串為：

L = {0123, 011223, 001233…}

1 的數量和 3 的數量相同，2 的數量和 1 的數量相同。

給定問題的 PDA 構造

PDA 如下：

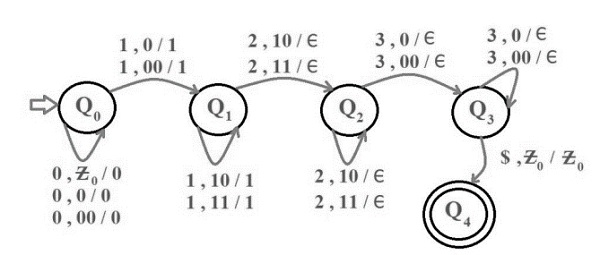
解釋

**步驟 1** - 首先將 0 入棧。

**步驟 2** - 接下來將 1 入棧。

**步驟 3** - 對於每個輸入的 2，彈出棧頂的一個 1。

**步驟 4** - 如果仍然有剩餘的 2，並且棧頂是 0，則該字串不被 PDA 接受。

**步驟 5** - 如果 2 已處理完畢，並且棧頂是 0，則對於每個輸入的 3，彈出相同數量的 0。

**步驟 6** - 如果字串處理完畢並且棧為空，則該字串被 PDA 接受。否則，該字串不被接受。

更新於：2021年6月15日

6K+ 次瀏覽

開啟你的職業生涯

完成課程獲得認證

開始學習
廣告