構建一個用於 L = {a^n b^n | n>=1} 的圖靈機。
圖靈機 (TM) 比有限自動機 (FA) 和下推自動機 (PDA) 都更強大。它們的強大程度與我們迄今為止構建的任何計算機一樣。
圖靈機的形式化定義
圖靈機可以形式化地描述為七元組
(Q,X, Σ, δ,q0,B,F)
其中,
Q 是有限的狀態集
X 是帶字母表
Σ 是輸入字母表
δ 是轉移函式:δ:QxX→QxXx{左移,右移}
q0 是初始狀態
B 是空白符號
F 是最終狀態。
圖靈機 (TM) 是一種數學模型,它由一條無限長的帶組成,該帶被分成單元格,輸入在這些單元格上給出。它包含一個讀取輸入帶的讀寫頭。一個狀態暫存器儲存圖靈機的狀態。
讀取輸入符號後,它會被替換為另一個符號,其內部狀態發生變化,並且它從一個單元格向右或向左移動。如果 TM 達到最終狀態,則接受輸入字串,否則拒絕。
圖靈機有一個讀/寫頭。所以我們可以在磁帶上寫入。
現在,讓我們構建一個接受相同數量的 a 和 b 的圖靈機,
它生成的語言是 L ={ anbn | n>=1},給定語言接受的字串為 -
L= {ab, aabb, aaabbb, aaaabbbb,………}
示例
考慮 n=3,所以 a3b3,磁帶看起來像 -

B= 空白
我們需要將每個 'a' 轉換為 X,並將每個 'b' 轉換為 Y。如果圖靈機包含相等數量的 X 和 Y,則它將到達最終狀態。
步驟 1 - 將初始狀態視為 q0。此狀態將 'a' 替換為 X 並向右移動,現在狀態從 q0 更改為 q1,因此轉移函式為 -
δ(q0, a) = (q1,X,R)

步驟 2 - 向右移動,直到看到空白符號。
δ(q1, a) = (q1,a,R) δ(q1, b) = (q1,b,R)
到達空白符號 B 後,向左移動並將狀態更改為 q2,因為我們需要將最後一個 'b' 更改為 Y。
δ(q1, B) = (q2,B,L) //1st iteration δ(q1, Y) = (q2,Y,L) // remaining iterations

步驟 3 - 當我們看到符號 'b' 時,將其替換為 Y 並將狀態更改為 q3 並向左移動。
δ(q2, B) = (q3,Y,L)

步驟 4 - 向左移動直到到達符號 X。
δ(q3, a) = (q3,a,L) δ(q3, b) = (q3,b,L)
當我們到達 X 時,向右移動並將狀態更改為 q0,並開始下一次迭代。
在透過將狀態從 q0 更改為 q4 將每個 'a' 和 'b' 替換為 X 和 Y 後,我們得到以下結果 -
δ(q0, Y) = (q4,Y,N)
N 表示不動。
| X | X | X | Y | Y | Y | B | B | ....................... |
q4 是圖靈機的最終狀態,q0 是圖靈機的初始狀態,中間狀態為 q1、q2、q3。
轉移圖
圖靈機的轉移圖如下 -
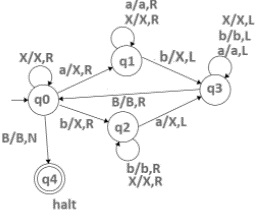


 資料結構
資料結構 網路
網路 關係型資料庫管理系統
關係型資料庫管理系統 作業系統
作業系統 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 語言程式設計
C 語言程式設計 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP