資料結構
網路
RDBMS
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究構建用於減法的圖靈機
圖靈機是一個七元組
(Q, Σ,Γ, δ,q0,qacc, qrej)
其中，
- Q 是有限數量的狀態
- Σ 是輸入字母表，不包含空白符號 t；
- Γ 是帶字母表，其中 t ε Γ 且 Σ ⊆ Γ；
- δ: (Q × Γ) → (Q × Γ × {L, R}) 是轉移函式；
- q0 ε Q 是起始狀態；
- qacc ε Q 是接受狀態；
- qrej ε Q 是拒絕狀態，其中 qrej ≠qacc。
問題
構建一個用於兩個一元整數減法的圖靈機 (TM)。
解決方案
兩個一元整數的減法
3-2=1
在圖靈機中，3 表示 - 111
2 表示：11
令 'M' 為用於分隔兩個整數的符號
| B | 1 | 1 | 1 | M | 1 | 1 | B |
這裡 B= 空白
M= 用於分隔兩個整數的符號
演算法
按照以下分步演算法構建用於減法的 TM：
步驟 1 - 將兩個一元整數作為輸入。我們從初始狀態 q0 開始。
步驟 2 - 如果我們在字串中找到 1，則轉到相同的狀態，不更改 1 的值，並轉到字串的右側。
步驟 3 - 如果我們找到 m 符號，則忽略此符號，不更改符號，並轉到字串的右側。
步驟 4 - 如果我們在經過 M 符號後找到 1，則將 1 的值更改為 X 並轉到字串的左側。
步驟 5 - 然後經過 M 符號並向左移動，如果我們找到 1，則將 1 的值更改為 X 並向右移動。
步驟 6 - 因此，在符號 (M) 之後，我們將所有 1 的值更改為 X，並且在符號 M 之前將相同數量的 1 更改為 X。
步驟 7 - 應用這些步驟並獲得兩個一元整數減法的圖靈機。
在處理減法時，圖靈機根據使用者提供的輸入考慮三種情況中的任何一種。
如果 'a' 和 'b' 是兩個整數，我們需要考慮：
- a>b
- a<b
- a=b
透過考慮所有三種情況，最終的圖靈機如下所示：
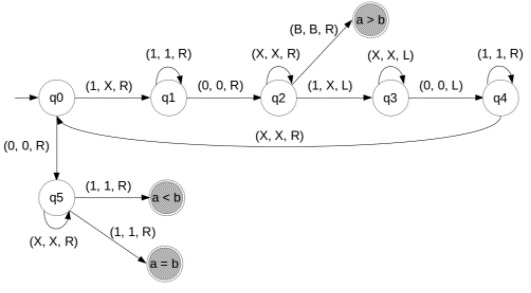
圖解說明
步驟 1 - 將輸入字串視為 110111
即 a=11 且 b=111，根據給定的輸入 a
步驟 2 - 從左到右掃描字串。
步驟 3 - 將 '1' 標記為 'X'，然後向右移動。
步驟 4 - 到達 '0' 的右側，並將 '1' 標記為 'X'，然後向左移動。
步驟 5 - 到達 '0' 左側的 'X'，然後向右移動一步。
步驟 6 - 再次將 '1' 標記為 'X'，然後向右移動。
步驟 7 - 到達 '0' 的右側並經過 'X'，將 '1' 標記為 'X'，然後向左移動。
步驟 8 - 到達 '0' 左側的 'X'，然後向右移動一步。
步驟 9 - 如果 'X' 之後存在 '0'，則表示 '0' 之前的 '1' 都已完成。
步驟 10 - 經過 '0'、'X'，並且還有 '1' 剩餘。也就是說，第二個數字大於第一個數字。
步驟 11 - 然後最終狀態為“a<b”
9K+ 瀏覽量
