資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
時尚學
法律學構造正則語言 L = (0+1)*(00+ 11) 的 ∈-NFA
非確定有限自動機 (NFA) 中的 ε 轉移用於在沒有來自輸入集 Σ 的任何符號的情況下從一個狀態移動到另一個狀態。
ε-NFA 定義為五元組
{Q, q0, Σ, δ, F}其中，
δ − Q × (Σ∪ε)→2Q
Q − 有限狀態集
Σ − 有限輸入符號集
q0 − 初始狀態
F − 終結狀態
δ − 轉移函式
沒有 ε 轉移的 NFA
NFA 以 5 元組表示法定義
{Q, q0, Σ, δ, F}其中，
δ − Q X Σ→ 2Q
Q − 有限狀態集
Σ, − 有限輸入符號集
q0 − 初始狀態
F − 終結狀態
δ − 轉移函式
NFA 和帶有 epsilon 的 NFA 幾乎相同；唯一的區別在於它們的轉移函式。
讓我們考慮給定的語言 L = 0(0+1)*1
構造 ε-NFA 的規則如下：
步驟 1 − 下面給出了 0+ 的帶 epsilon 的 NFA：
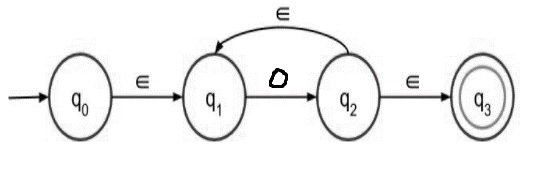
步驟 2 − 下面給出了 0* 的帶 epsilon 的 NFA：
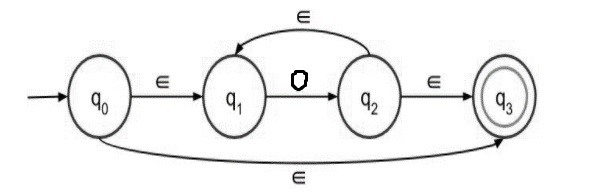
步驟 3 − 下面給出了 (0+1) 的帶 epsilon 的 NFA：
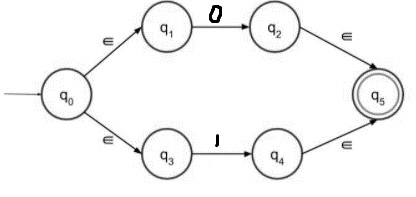
上面的狀態轉換圖接受 0 或 1 作為輸入。這兩條路徑都通向終結狀態。
步驟 4 − 下面給出了 01 的帶 epsilon 的 NFA：
對於連線，0 必須後跟 1。
步驟 5 −
L = (0+1)*(00 + 11) 的 ε-NFA
L = (0+1)*(00 + 11) 分為兩部分：(0+1)* 和 (00+11)。
首先構造第一部分，然後構造第二部分，最後連線這兩部分以獲得結果。
第一部分 − (0+1)*
藉助步驟 3，我們可以輕鬆地構造 (0+1)*，如下所示：
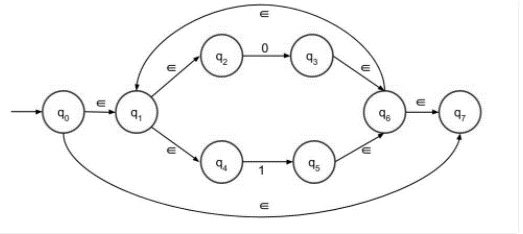
第二部分 − (00+11)
第二部分可以藉助步驟 4 輕鬆繪製。
在步驟 4 中，考慮 1 和 0 都是 00 或 11。這兩個字串由 + 符號連線。
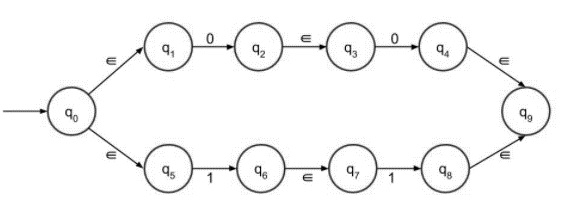
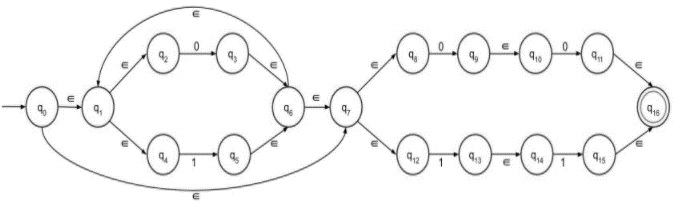
最終帶有 epsilon 移動的 NFA 如下：
連線第一部分和第二部分，
更新於： 2021年6月14日
17K+ 次檢視
廣告