中心八面體數

---

中心八面體數是什麼意思？讓我們來解讀一下。

首先，什麼是八面體？

八面體是一個具有八個面、等邊三角形形狀的三維幾何圖形。它是一個多面體，具有8個頂點、12條邊和6個正方形面。它是五個柏拉圖立體之一，這些立體都是規則的凸多面體，具有對稱的頂點排列和相同的邊。

八面體具有各種引人入勝的特性和用途，包括晶體學，其中它用於描述某些晶體的結構；以及計算機圖形學，其中它用於對三維物體建模。許多其他自然現象，包括某些病毒的結構和某些晶體的形狀，也表現出八面體形狀。

請看下面的圖表，您將清楚地瞭解什麼是八面體。

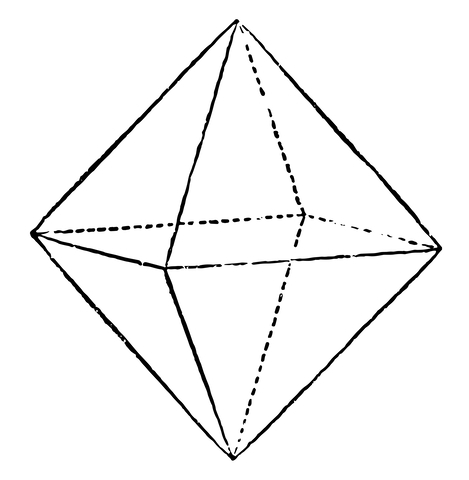
現在，什麼是八面體數？

八面體數是一個形象數，表示在八面體中均勻分佈的點數。換句話說，它是構建具有特定層數球體的八面體所需的球體數量。

以下是最初的八面體數

1, 6, 19, 44, 85, 146, 231, 344, 489, 670, ...

八面體數的應用可以在許多領域找到，包括晶體學、化學和幾何學。例如，它們用於指定可以圍繞中心原子聚集在特定型別的化學結構中的原子數。

請看下面的圖表以瞭解八面體數。

接下來，什麼是中心八面體數？

中心八面體數是指在以原點為中心的八面體中均勻分佈的點數。換句話說，它是三維立方晶格中以原點為中心的八面體內的格點數。

以下是最初的幾個中心八面體數

1, 7, 25, 63, 129, 231, 377, 575, 833, 1159, ...

中心八面體數的公式可以透過使用前n箇中心平方數的和的公式得到，該公式為：

Sn = n(2n−1)(2n+1)/3

將前n箇中心平方數相加，然後乘以2，可以得到第n箇中心八面體數

Co_n = 2Sn = 2n(2n−1)(2n+1)/3

簡化這個表示式，我們得到

Co_n = (2n+1)(2n^2+2n+3)/3

中心八面體數用於表示在特定型別的化學結構中可以圍繞中心原子聚集的原子數。它們在許多領域都有用，包括晶體學。它們也與二維格路計數德拉努瓦數有關。

方法

以下是計算中心八面體數的分步方法。

• 指定或獲取n作為使用者輸入

• 使用公式 Co_n = (2n+1)(2n^2+2n+3)/3 計算中心八面體數

• 將中心八面體數列印到控制檯。

C++ 實現

理論太多？現在讓我們開始編碼。讓我們將上面討論的方法轉換為C++程式碼。

示例

#include <iostream>
using namespace std;

int centered_octahedral(int n) {
    return (2 * n + 1) * (2 * n * n + 2 * n + 3) / 3;
}

int main() {
    int n= 6;
    
    cout << "The " << n << "th centered octahedral number is: " << centered_octahedral(n) << endl;
    return 0;
}

輸出

The 6th centered octahedral number is: 377

時間複雜度：O(1)

空間複雜度：O(1)

結論

在本文中，我們詳細介紹了中心八面體數以及計算第n箇中心八面體數的方法。希望您現在對這個概念有了清晰的瞭解。