
- 自動機理論教程
- 自動機理論 - 首頁
- 自動機理論 - 入門
- 自動機理論 - 歷史
- 自動機理論 - 應用
- 自動機理論術語
- 自動機中字串的基礎
- 自動機的集合論
- 語言和文法
- 計算理論中的文法
- 由文法生成的語言
- 喬姆斯基文法分類
- 有限自動機
- 確定性有限自動機 (DFA)
- 非確定性有限自動機 (NFA)
- 從 NFA 到 DFA 的轉換
- DFA 的最小化
- 穆爾機與米利機
- DFA 的補集
- 正則表示式
- 自動機中的正則表示式
- 自動機中的 Arden 定理
- 將正則表示式轉換為有限自動機
- 正則文法的泵引理
- 計算理論中的正則集
- 上下文無關文法
- 上下文無關文法 (CFG)
- 上下文無關文法中的二義性
- 上下文無關語言的封閉性
- 簡化上下文無關文法
- 喬姆斯基正規化 (CNF)
- 格雷巴赫正規化 (GNF)
- 上下文無關文法的泵引理
- 下推自動機
- 下推自動機 (PDA)
- 下推自動機的接受
- 從 CFG 構造 PDA
- 下推自動機和語法分析
- 圖靈機
- 圖靈機 (TM) 基礎
- 圖靈機接受的語言
- 多磁帶圖靈機
- 多軌跡圖靈機
- 非確定性圖靈機
- 半無限磁帶圖靈機
- 線性界限自動機 (LBA)
- 可計算性和不可判定性
- 圖靈語言的可判定性
- 不可判定語言
- 圖靈機停機問題
- 計算理論中的 Rice 定理
- Post 對應問題 (PCP)
- 自動機理論資源
- 自動機理論 - 快速指南
- 自動機理論 - 資源
- 自動機理論 - 討論

自動機理論教程
自動機理論是計算機科學的一個分支,它處理設計抽象的、自動驅動的計算裝置,這些裝置自動遵循預定的操作序列。
一個狀態數有限的自動機稱為有限自動機。這是一個簡短而簡潔的教程,在介紹圖靈機和可判定性之前,介紹了有限自動機、正則語言和下推自動機的基本概念。
誰應該學習自動機理論?
本教程是為攻讀任何資訊科技或計算機科學相關領域學位的學生準備的。它旨在幫助學生掌握自動機理論中涉及的基本概念。
學習自動機理論的先決條件
本教程在理論和數學嚴謹性之間取得了良好的平衡。讀者應該具備離散數學結構的基本理解。
什麼是自動機理論?
在數學和計算機科學中,自動機理論處理抽象機器和計算問題。自動機是自動遵循預定操作的自驅動計算裝置。
根據約翰·馮·諾依曼的說法,“自動機理論是一種邏輯理論,它處理自動機和資訊的研究,強調需要一個詳細的、數學的和分析的理論來理解複雜的自動機。”
什麼是自動機?
自動機是一種有限尺寸的裝置,具有指定的輸入和輸出,其行為由輸入決定。換句話說,自動機指的是自動執行的機械物體,它們根據預定的指令或程式轉換資訊。
自動機也可以指代一類機電裝置,既有理論上的,也有現實中的,它們在被啟動後轉換資訊。
自動機的主要型別是什麼?
自動機可以分類如下:
- 有限自動機 - 有限自動機是一種狀態數有限的自動機,它根據輸入符號串改變其狀態。當搜尋到期望的符號時,就會發生轉換。
- 下推自動機 - 下推自動機 (PDA) 是一種基於棧的自動機,用於計算理論。它比有限狀態機更強大,可以解決比 FA 更復雜的問題。
- 圖靈機 - 圖靈機是一種理論裝置,它使用規則表來操作磁帶上的一系列符號,該磁帶由無限長的磁帶組成,磁帶被分成包含 1、0 或空位的單元格。
- 線性界限自動機 - 線性界限自動機 (LBA) 是一種圖靈機,它只使用輸入磁帶空間,這與圖靈機不同。它的長度是輸入長度的線性函式,並且讀寫頭只能訪問磁帶的有限連續部分。
- 元胞自動機 - 元胞自動機是確定性系統,它們在離散的時間和空間中演化,通常是網格。它們由區域性更新的單元格組成,這些單元格遵循全域性時間尺度和遞迴規則,在網格上同步更新。
什麼是有限自動機?
有限狀態機 (FSM)是一種計算的數學模型,在任何給定時間都可以處於有限數量的狀態之一。它可以根據輸入(稱為轉換)從一個狀態更改為另一個狀態。
FSM 由其狀態、初始狀態和輸入定義。FSM 有兩種型別:確定性和非確定性。對於任何非確定性 FSM,都可以構造出一個等價的確定性 FSM。
確定性和非確定性有限自動機之間的區別
下表突出了確定性和非確定性有限自動機之間的主要區別:
| 方面 | 確定性有限自動機 | 非確定性有限自動機 |
|---|---|---|
| 狀態轉換 | 每個輸入都唯一地確定結果狀態 | 某些輸入可能允許選擇結果狀態 |
| 可預測性 | 最終狀態完全由輸入詞確定 | 對於給定的輸入詞,可能有幾個可能的最終狀態 |
| 空轉換 | 僅在讀取輸入後才能更改狀態 | 可以在不讀取任何輸入的情況下更改狀態 |
| 初始狀態 | 一個初始狀態 | 可能有多個初始狀態 |
| 詞接受 | 如果最終狀態是接受狀態,則接受該詞 | 如果至少一個可能的最終狀態是接受狀態,則接受該詞 |
| 狀態佔用 | 一次處於一個狀態 | 可以認為同時處於多個狀態 |
什麼是下推自動機?
下推自動機是非確定性有限狀態機,其額外記憶體採用棧的形式。它比 FSM 更強大,但比圖靈機弱。它們接受上下文無關語言。
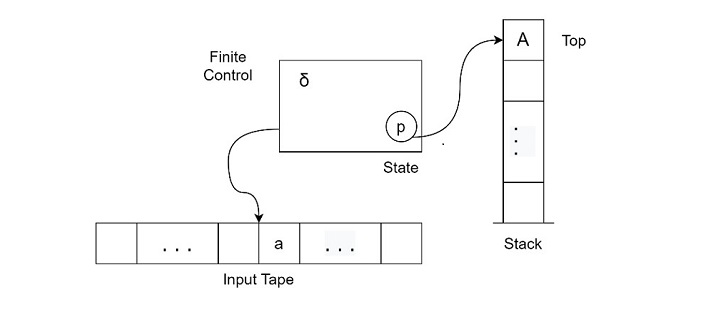
例如,為了確保程式碼有效,程式設計師可以將程式碼輸入到一個下推自動機中,該自動機使用實現平衡括號語言的上下文無關文法的轉移函式進行程式設計。如果程式碼有效且所有括號都匹配,則下推自動機將接受該程式碼。如果存在不平衡的括號,則自動機可以返回程式碼的無效性。
什麼是圖靈機?
圖靈機是一種抽象的計算模型,它透過讀寫無限長的磁帶來執行計算。它為解決計算機科學問題和測試計算的極限提供了強大的計算模型。圖靈機是由艾倫·圖靈在 1936 年發明的。
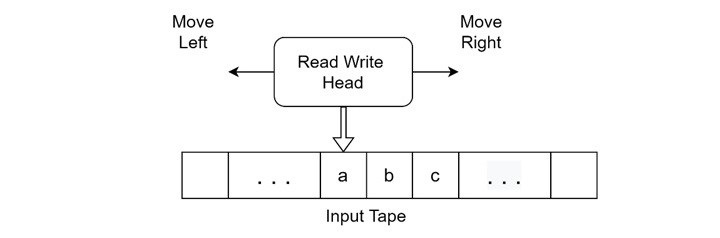
圖靈機由無限長的磁帶、磁頭和狀態轉移表組成。它們在輸入位串上執行,磁頭處於某個狀態,表控制其行為。
圖靈機可以模擬程式的複雜性和其對記憶體中不同資料的反應。
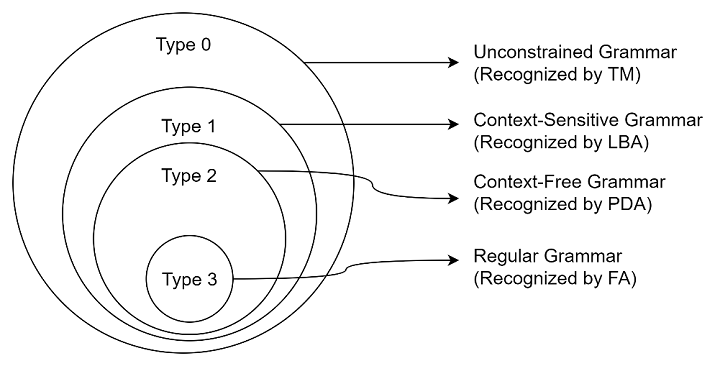
什麼是喬姆斯基層次結構?
喬姆斯基層次結構是計算機科學和語言學中的一個分類系統,它包含四個級別:
- 0 型(無限制)
- 1 型(上下文相關)
- 2 型(上下文無關)
- 3 型(正則)
以諾姆·喬姆斯基命名,它描述了不同型別形式語言和文法的表達能力。它是形式語言研究中的一個基本概念,用於開發語法分析演算法和其他用於處理形式語言的工具。
什麼是上下文無關語言?
上下文無關語言 (CFL)是由上下文無關文法生成的,它與下推自動機接受的語言集相同。正則語言是上下文無關語言的子集,如果輸入語言以接受的最終狀態結束,則計算模型接受這些語言。
形式語言理論將語言定義為受特定規則約束的一組符號,例如書面英語。有效的句子必須遵循特定的語法規則。上下文無關語言是由上下文無關文法生成的語言,它可以由多個上下文無關文法生成,這使得它更通用和包容性。
$\mathrm{\lbrace a^{n}b^{n} \: | \: n > 0\rbrace}$ 是上下文無關文法的示例,它表示所有 a 和 b 個數相等的字串。例如 $\mathrm{a^{4}b^{4}}$ 是 aaaabbbb。
什麼是上下文相關語言?
上下文相關文法比上下文無關文法更強大,因為它們能夠描述某些上下文無關文法無法描述的語言。在喬姆斯基層次結構中,它們位於上下文無關文法和無限制文法之間。
上下文相關文法 (CSG) 允許生成規則被終結符和非終結符包圍。
$\mathrm{\lbrace a^{n}b^{n}c^{n} \: | \: n > 0\rbrace}$ 是一個CFG的例子,它表示所有 a、b 和 c 的數量相等的字串。例如 $\mathrm{a^{4}b^{4}c^{4}}$ 是 aaaabbbbcccc。要透過 CSG 生成這種語言,需要在生成過程中跟蹤左右上下文。
什麼是遞迴可列舉語言?
遞迴可列舉 (RE) 語言,也稱為 0 型語言,由 0 型文法生成,並且可以被圖靈機接受或識別。
對於語言的字串,RE 語言可以進入最終狀態;對於非語言字串,它可能進入或可能不進入拒絕狀態。對於非語言字串,圖靈機可能會永遠迴圈,這使得它們成為圖靈可識別語言。
這些字串可能執行以下操作之一:
- 停止並接受
- 停止並拒絕
- 永遠迴圈
遞迴可列舉的另一個子集是遞迴語言,它可以被全圖靈機接受,並且將在以下兩種情況之一中停止:“停止並接受”或“停止並拒絕”。
抽運引理的意義是什麼?
抽運引理 是一種引理(通常是較小的、經過證明的命題,可以用作通往更大結果的墊腳石),我們透過反證法來證明某些東西。在 TOC 中,抽運引理用於反證某種語言是正則的或上下文無關的(如果我們對 CFG 使用抽運引理)。
抽運引理可以作為一種工具來證明某些語言不是正則的或不是上下文無關的。透過應用抽運引理,我們可以證明某些語言不能被有限自動機或下推自動機識別。這在理論計算機科學和形式語言理論中特別有用,用於確定這些計算模型的侷限性。
抽運引理有助於對語言進行分類,並瞭解不同型別的自動機的功能和約束。
在形式語言的上下文中,什麼是文法?
形式文法是形式語言中字串的一組生成規則,定義哪些字串根據語言的語法是有效的,而不是它們的含義或上下文。它專注於形式語言中這些字串的形式。
它表示為 G(V, N, P, S)。它生成字母表上所有句法上正確的字串,主要用於語法分析階段,特別是在編譯期間,在編譯階段。
G = (V, N, P, S) 是一個文法,其中:
- N 是非終結符的有限集合
- V 是終結符的有限集合
- P 描述一組生成規則
- S 是起始符號
語言和文法之間的區別
文法是一組生成規則,用於生成語言的字串。文法 不過是符號、生成規則和起始符號的集合,透過四元組 G = (V, N, P, S) 表示。
另一方面,語言是文法的產物。如果沒有定義文法,我們就無法建立語言。在下面的示例中,展示了文法和該文法使用的語言的概念。
$$\mathrm{G \: = \: (V,N,P,S) \: = \: (\lbrace S,A,B,C \rbrace , \: \lbrace a,b,c \rbrace , \: \lbrace S \rightarrow ABC, \: A\rightarrow a, \: B\rightarrow b, \: C\rightarrow c \rbrace , \: \lbrace S \rbrace)}$$
透過此文法可以形成一個可能的語言 L(G),L(G) = {abc}
從 S → ABC、A → a、B → b 和 C → c,它將生成“abc”,這是一個語言。
可判定問題和不可判定問題之間的區別
對於可判定問題,演算法可以為任何給定例項提供明確的答案,例如“是”或“否”,而不可判定性指的是沒有演算法可以為所有可能的例項提供明確答案的問題。
| 方面 | 可判定問題 | 不可判定問題 |
|---|---|---|
| 定義 | 存在用於明確答案的演算法 | 在所有情況下都沒有用於明確答案的演算法 |
| 答案 | 明確的“是”或“否” | 缺乏所有例項的明確答案 |
| 演算法 | 存在有效的求解演算法 | 沒有適用於所有例項的演算法 |
| 時間 | 在合理的時間內給出有限的答案 | 可能不會對所有輸入都終止 |
| 證明 | 透過演算法的存在性證明 | 透過嚴格的數學證明證明 |
| 影響 | 允許有效的解決問題 | 提出根本性挑戰 |
| 示例 | 語言成員資格、排序 | 停機問題、考拉茲猜想 |
什麼是停機問題?
停機問題是可計算理論中的一個判定問題,用於確定計算機程式是否會終止或永遠執行。
例如,如果我們從使用者那裡獲取一個正數“x”(x > 0),並在 while 迴圈中檢查“x”是否為 0,在迴圈中我們不更新“x”的值。這將永遠不會停止。
停機問題是一個眾所周知的問題,已被證明是不可判定的,這意味著沒有程式可以解決足夠通用的計算機程式的停機問題。
圖靈機在計算理論中經常被用作與“普通計算機”一樣強大的工具。1936 年,艾倫·圖靈使用圖靈機證明了圖靈機上的停機問題是不可判定的,這意味著沒有圖靈機可以正確地決定所有可能的程式/輸入對。
在計算複雜度中,P 類和 NP 類是什麼?
P 是一種複雜度類,它包含可以使用確定性圖靈機在多項式時間內解決的判定問題。它通常被認為是“有效可解”或“易處理的”計算問題。
難處理問題在理論上是可解的,但在實踐中無法解決。P 包含諸如計算最大公約數、查詢最大匹配等自然問題,確定一個數是否為素數也屬於 P。
NP 或非確定性多項式時間是一組在非確定性圖靈機上可以在多項式時間內解決的判定問題。這些問題可以透過確定性圖靈機在多項式時間內進行驗證。一些示例包括布林可滿足性問題 (SAT)、哈密頓路徑問題(TSP 的特例)、頂點覆蓋問題等。
NP 完全問題和 NP 難問題之間的區別
在計算理論中,如果存在一個現有的 NP 完全問題 Y 可以被在多項式時間內規約到問題 X,則問題 X 可以稱為 NP 難。
NP 難問題的難度級別類似於 NP 完全問題。但是,NP 難問題不一定要屬於 NP 類。一個問題只有在同時屬於 NP 難和 NP 問題時才能成為 NP 完全問題。
| 方面 | NP 難 | NP 完全 |
|---|---|---|
| 含義 | 解決 NP 難問題 X 需要存在一個 NP 完全問題 Y,該問題可以在多項式時間內規約到問題 X。 | 當存在一個 NP 問題 Y 在多項式時間內可規約到 X 時,問題 X 為 NP 完全。 |
| NP 類 | 不需要在 NP 類中 | 必須在 NP 類中 |
| 關係 | NP 完全是 NP 難的子集 | 必須同時是 NP 和 NP 難 |
| 示例 |
電路滿意度 頂點覆蓋 |
圖中哈密頓迴路的確定 布林公式可滿足性問題。 |
在自動機的上下文中,什麼是轉移函式?
在自動機理論的上下文中,有一些表格包含狀態、輸入符號、起始狀態、最終狀態集和轉移函式。
(Q, Σ, q0, F, T),其中 Q 是狀態集,Σ 是輸入符號。
當狀態 q 從集合 Σ 中獲取輸入時,它會從 q 傳送到另一個集合 q' 或 q 本身。基於輸入的轉換在轉移函式中定義。轉移函式集在集合 T 中提及。
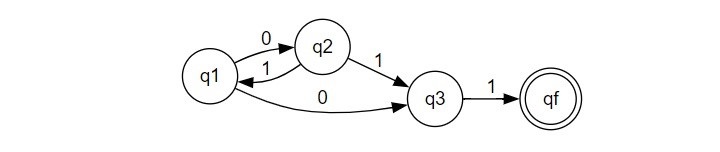
在這個狀態圖中,有幾個轉換,其中一些可能是:
$$\mathrm{\delta(q1, 0) \: \rightarrow \: q2}$$
$$\mathrm{\delta(q3, 1) \: \rightarrow \: qf}$$
什麼是狀態圖?
自動機理論中的狀態圖是有限自動機行為的視覺化表示。
它由表示狀態的頂點 (集合 Q)、輸入符號 (Σ) 和輸出符號 (Z)(如果沒有輸出集,它可以具有 Q 的子集、F 最終狀態或接受狀態的集合以及一組轉換 T)組成。
它用於透過顯示可能的狀態和這些狀態之間的轉換來描述和分析系統行為。狀態圖提供了一種清晰簡潔的方法來理解有限自動機的可能狀態和轉換。
這是一個狀態圖示例:
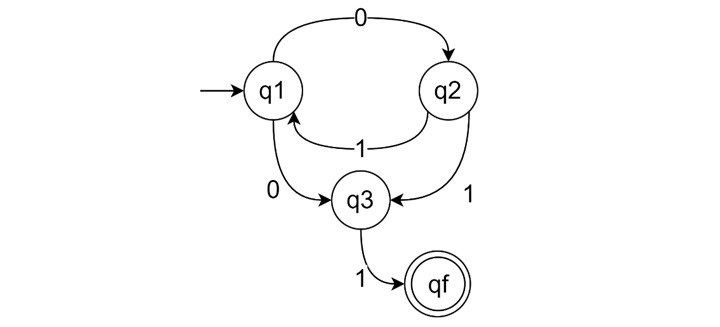
這裡我們有四個狀態
- Q = {q1, q2, q3, qf}
- 最終狀態 F = {qf}
- 輸入 Σ = {0, 1}
- 初始狀態 q1
並且,
$$\mathrm{T \: = \: \lbrace \delta(q1, 0) \: \rightarrow \: q2, \: \delta(q1, 0) \: \rightarrow \: q3, \: \delta(q2, 1) \: \rightarrow \: q1, \: \delta(q2, 1) \: \rightarrow \: q3, \: \delta(q3, 1) \: \rightarrow \: qf \rbrace}$$
狀態在自動機中的意義是什麼?
自動機理論用於概念化一個系統,有助於在現實生活中設計它。它必須具有與輸入相關的輸入、輸出和轉換。狀態圖中狀態是表示系統有限數量的條件或情況的基本元件。
狀態對於分析和表示系統的行為、跟蹤物件的不同條件至關重要。一組有限的狀態描述了自動機響應輸入符號的行為。這種基於狀態的方法對於可以抽象成有限數量的不同條件的系統特別有用。
什麼是確定性下推自動機?
確定性下推自動機 (DPDA 或 DPA) 是自動機理論中下推自動機的變體,它接受確定性上下文無關語言。
此處,機器轉換基於當前狀態、輸入符號和棧頂符號,較低層級的符號不會產生直接影響。機器操作包括入棧、出棧或替換棧頂元素。
正式地講,對於一個 PDA 機器,**M = (Q, Σ, Γ, δ, q0, z, F)** 是確定的,如果對於每個 **q ∈ Q, a ∈ Σ ∪ {λ}, b ∈ Γ**
- **δ(q, a, b)** 至多隻有一個元素。
- 如果 **δ(q, λ, b)** 非空,則對於每個 **c ∈ Σ**,**δ(q, c, b)** 必須為空。
什麼是非確定性下推自動機?
非確定性下推自動機 (NPDA) 是一種機器,它擁有 NFA 和棧的所有特性。它的程式利用當前狀態、讀寫頭下的當前符號以及棧頂符號來做出決策。NPDA 比確定性 PDA 更強大。
NPDA 中的棧與輸入帶的“語言”字母表是不同的。棧在控制自動機的起始狀態使用,棧中只有初始符號。
在每一步中,狀態、輸入元素和棧頂符號決定下一步(轉換)。轉換步驟包括改變狀態、從輸入帶讀取符號、向右移動到下一個符號以及修改棧。
什麼是通用圖靈機?
圖靈機是一種數學工具,等價於數字計算機(圖靈,20世紀30年代)。它包含一個機器計算的輸入輸出關係,輸入以二進位制形式給出在機器的帶上。輸出包括機器停止時帶的內容。帶的內容由圖靈機內部的有限狀態機 (FSM) 決定。
然而,圖靈機需要為每個新的計算和輸入輸出關係構建一個不同的圖靈機。這導致了通用圖靈機 (UTM) 的發明,它接收機器 M 的描述,並可以在輸入帶剩餘內容上模擬它。
請檢視以下通用圖靈機的概念圖 -
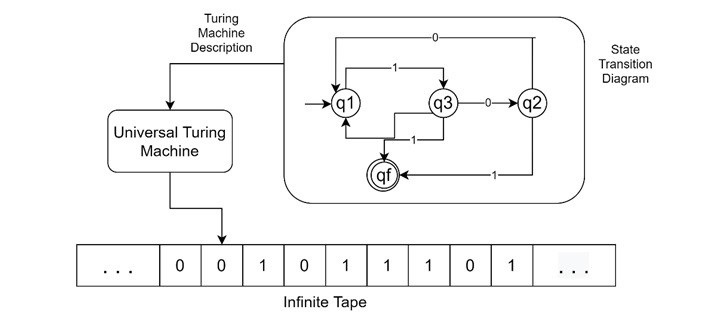
在這裡,我們使用無限長的帶,UTM 在上面工作,但此外它還從一個單獨的模組中獲取機器描述或狀態轉換到 UTM 模組,在實現中,帶本身在單獨的區域儲存機器描述。
為什麼在計算機科學中使用形式語言?
在計算機科學中,形式語言是在一個有限的符號集(稱為字母表)上的一組字串,並且使用此字母表根據定義的語法規則建立的結構化字串構成了形式語言。
形式語言圍繞三個關鍵概念構建:字母表、字串和語法。
- **字母表**是有限的一組不同的符號,
- **字串**是從字母表中選擇的一系列有限符號。符號的順序在字串中很重要,空字串包含零個符號。
- **語法**是一組正式規則,用於控制符號的組合以構成形式語言中的字串。
這些規則對於不同類別的形式語言(如正則語言、上下文無關語言、上下文相關語言和遞迴可列舉語言)是不同的。
自動機在解析中的作用是什麼?
解析是一個基於語法的過程,它使用產生式規則推匯出一個字串並檢查其可接受性。它是一個用於檢查字串是否在語法上正確的工具。
解析器可以是自頂向下或自底向上,從頂部開始使用開始符號並使用語法樹來推匯出字串。
自頂向下解析
- PDA 使用自頂向下解析將語法的開始符號與其棧中的輸入進行匹配。
- 如果它是一個終結符,則將其與當前輸入符號進行比較,
- 如果它是非終結符,則用產生式規則替換。
- 棧跟蹤解析上下文和預期符號,如果棧為空並且所有輸入都被消耗,則接受輸入。
自底向上解析
- PDA 從一個空棧開始並讀取輸入符號。
- 它透過移進-歸約動作將序列簡化為非終結符。
- 棧包含部分構建的語法樹,如果在所有輸入都被消耗時存在開始符號,則接受輸入。
什麼是線性有界自動機?
一個線性有界自動機是一個多軌道的非確定性圖靈機,其帶的長度有限。線性有界自動機中的計算被限制在一個恆定的有界區域內,其中兩個特殊的符號充當左右端標記。
確定性線性有界自動機是上下文相關的,而具有空語言的線性有界自動機是不可判定的。
非確定性線性邊界演算法 (LBA) 與上下文相關語言的關係與下推自動機與上下文無關語言的關係相同。
目前尚不清楚 LBA 的確定性版本是否與非確定性版本具有相同的功效。
它是一個 9 元組自動機:G = (Q, Σ, Γ, δ, q0, B, F, GL, GR)
- Q - 狀態集
- Σ - 輸入字母集
- Γ - 帶字母 Σ ⊂ Γ
- δ - 轉換函式集
- q0 - 初始狀態
- B - 空白符號集,B ∈ Γ – Σ
- F - 終結狀態集 F ⊂ Q
- GL - 左端標記 GL ∈ Σ
- GR - 右端標記 GR ∈ Σ
Myhill-Nerode 定理的意義是什麼?
Myhill-Nerode 定理指出,如果語言L的L~(L~是字串x和y上的關係,其中x和y沒有可區分的擴充套件)具有有限數量的等價類,並且如果此數量為N,則存在一個識別 L 的最小確定性有限自動機 (DFA),其中包含N個狀態。
除了定義之外,Myhill-Nerode 定理還用於解釋哪些語言可以被簡單的機器或“有限狀態自動機”識別。它有助於理解這些簡單的機器可以處理哪些語言,或者可以在機器上進行多少簡化以接受這些語言。
自動機和語法的等價性是什麼?
等價性表示不同型別的自動機與其可以識別的語法類別之間的關係。根據喬姆斯基的分類,有四種類型的語法。
| 語言 | 自動機 |
|---|---|
| 遞迴可列舉語言:等價於 0 型語法 | 被圖靈機識別 |
| 上下文相關語言:等價於 1 型語法 | 被線性有界自動機 (LBA) 識別 |
| 上下文無關語言:等價於 2 型語法 | 被下推自動機 (PDA) 識別 |
| 正則語言:等價於 3 型語法 | 被有限狀態自動機 (FSA) 識別 |
什麼是正則表示式?
喬姆斯基分類中的 3 型語法也被稱為正則語法。有限自動機可以透過簡單的表示式(稱為正則表示式)來接受正則語言。
正則表示式是表示任何語言的最有效方法。這些表示式定義一個字串並匹配字元組合。字串搜尋演算法使用此模式查詢字串上的操作,從而易於檢查語言。
正則表示式,用x*表示,表示x的零次或多次出現,而x+表示x的一次或多次出現,生成一系列字元。
(a | b)*表示任何大小的a和b的所有可能組合。[此處符號“|”表示或]
正則表示式如何與有限自動機相關?
正則表示式是一種被有限自動機接受的語言描述語言,它提供了任何語言的最有效表示,其中Σ表示輸入集作為字母表。它可以定義如下 -
- Φ表示空集,
- ε表示空字串,
- 對於Σ中的每個'a',都是一個正則表示式,並表示集合'a'。
如果“r”和“s”是分別表示語言 L1 和 L2 的正則表示式,則
- “r + s”與 (L1 ∪ L2) 相同
- rs與L1L2串聯相同
- r*分別等價於L1*閉包

該圖演示了將 RE 輕鬆轉換為具有 epsilon 移動的非確定性有限自動機 (NFA),然後轉換為確定性有限自動機 (DFA),然後可以輕鬆地將其轉換為 RE。
閉包性質在自動機理論中的重要性是什麼?
自動機理論和形式語言中的閉包性質是指在對其成員執行某些操作後,語言類別仍然保持在該類別內。
在正則語言的上下文中,當透過並集或串聯等操作執行時,它們具有相同的特徵和限制,因此我們可以說正則語言在並集下是封閉的。
正則語言在並集、交集、串聯、補集和 Kleene 閉包等運算下是封閉的。相反,確定性 CFL 在補集、與正則語言的交集和逆同態下是封閉的。
什麼是非確定性圖靈機?
非確定性圖靈機 (TM) 對於每個狀態和符號都有一組動作,使得轉換是非確定性的。TM 的計算是一棵從起始配置開始的配置樹。
像 NTM 這樣的機器可以在每一步中進行多次轉換,例如從輸入符號轉換到狀態 Qi、Qj、Qk 等。NTM“猜測”最終導致接受狀態 Qf 的最佳轉換,因為每一步中都沒有建立良好的轉換。這個概念就像一個迷宮,機器總能猜出正確的選擇,如果存在一條路,就能找到最快的方法出去。
NTM 是計算機科學家理解計算極限、複雜性理論和有效演算法求解類別的寶貴工具。它們在研究 NP(非確定性多項式時間)和 NP 完全問題等複雜性類別中特別有用,使研究人員能夠推理那些解決方案可以有效驗證但可能難以找到的問題。但是,設計 NTM 在實踐中不像 DTM 那樣可行。