Python AI - 無監督學習：聚類

---

無監督機器學習演算法沒有任何監督者提供任何指導。這就是為什麼它們與某些人所說的真正人工智慧緊密相關的原因。

在無監督學習中，沒有正確答案，也沒有老師指導。演算法需要發現數據中有趣的模式才能學習。

什麼是聚類？

從根本上說，它是一種無監督學習方法，也是一種常用的統計資料分析技術，在許多領域得到應用。聚類主要是將觀測資料集劃分為子集（稱為簇）的任務，以便同一簇中的觀測值在某種意義上相似，並且與其他簇中的觀測值不同。簡單來說，我們可以說聚類的主要目標是根據相似性和差異性對資料進行分組。

例如，下圖顯示了不同簇中類似型別的資料：

用於聚類資料的演算法

以下是幾種常見的用於聚類資料的演算法：

K均值演算法

K均值聚類演算法是用於聚類資料的一種知名演算法。我們需要假設簇的數量已知。這也被稱為扁平聚類。它是一種迭代聚類演算法。此演算法需要遵循以下步驟：

步驟 1 – 我們需要指定所需的 K 個子組數量。

步驟 2 – 確定簇的數量，並隨機將每個資料點分配到一個簇中。或者換句話說，我們需要根據簇的數量對資料進行分類。

在此步驟中，應計算簇中心。

由於這是一種迭代演算法，因此我們需要在每次迭代中更新 K 箇中心的位，直到找到全域性最優值，或者換句話說，中心到達其最佳位置。

以下程式碼將有助於在 Python 中實現 K 均值聚類演算法。我們將使用 Scikit-learn 模組。

讓我們匯入必要的包：

import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
from sklearn.cluster import KMeans

以下程式碼行將有助於使用 sklearn.dataset 包中的 make_blob 生成包含四個斑點的二維資料集。

from sklearn.datasets.samples_generator import make_blobs

X, y_true = make_blobs(n_samples = 500, centers = 4,
            cluster_std = 0.40, random_state = 0)

我們可以使用以下程式碼視覺化資料集：

plt.scatter(X[:, 0], X[:, 1], s = 50);
plt.show()

在這裡，我們初始化 kmeans 為 KMeans 演算法，以及所需的簇數量引數 (n_clusters)。

kmeans = KMeans(n_clusters = 4)

我們需要使用輸入資料訓練 K 均值模型。

kmeans.fit(X)
y_kmeans = kmeans.predict(X)
plt.scatter(X[:, 0], X[:, 1], c = y_kmeans, s = 50, cmap = 'viridis')

centers = kmeans.cluster_centers_

下面給出的程式碼將幫助我們根據我們的資料繪製和視覺化機器的發現，以及根據要查詢的簇數量進行擬合。

plt.scatter(centers[:, 0], centers[:, 1], c = 'black', s = 200, alpha = 0.5);
plt.show()

均值漂移演算法

它是無監督學習中另一種流行且強大的聚類演算法。它不做出任何假設，因此它是一種非引數演算法。它也稱為層次聚類或均值漂移聚類分析。以下是此演算法的基本步驟：

• 首先，我們需要從分配到各自簇的資料點開始。

• 現在，它計算質心並更新新質心的位置。

• 透過重複此過程，我們更接近簇的峰值，即朝向密度較高的區域。

• 此演算法在質心不再移動的階段停止。

藉助以下程式碼，我們正在 Python 中實現均值漂移聚類演算法。我們將使用 Scikit-learn 模組。

讓我們匯入必要的包：

import numpy as np
from sklearn.cluster import MeanShift
import matplotlib.pyplot as plt
from matplotlib import style
style.use("ggplot")

以下程式碼將有助於使用 sklearn.dataset 包中的 make_blob 生成包含四個斑點的二維資料集。

from sklearn.datasets.samples_generator import make_blobs

我們可以使用以下程式碼視覺化資料集

centers = [[2,2],[4,5],[3,10]]
X, _ = make_blobs(n_samples = 500, centers = centers, cluster_std = 1)
plt.scatter(X[:,0],X[:,1])
plt.show()

現在，我們需要使用輸入資料訓練均值漂移聚類模型。

ms = MeanShift()
ms.fit(X)
labels = ms.labels_
cluster_centers = ms.cluster_centers_

以下程式碼將列印簇中心和根據輸入資料預測的簇數量：

print(cluster_centers)
n_clusters_ = len(np.unique(labels))
print("Estimated clusters:", n_clusters_)
[[ 3.23005036 3.84771893]
[ 3.02057451 9.88928991]]
Estimated clusters: 2

下面給出的程式碼將幫助我們根據我們的資料繪製和視覺化機器的發現，以及根據要查詢的簇數量進行擬合。

colors = 10*['r.','g.','b.','c.','k.','y.','m.']
   for i in range(len(X)):
   plt.plot(X[i][0], X[i][1], colors[labels[i]], markersize = 10)
plt.scatter(cluster_centers[:,0],cluster_centers[:,1],
   marker = "x",color = 'k', s = 150, linewidths = 5, zorder = 10)
plt.show()

衡量聚類效能

現實世界中的資料並非自然地組織成多個不同的簇。由於這個原因，不容易進行視覺化和推斷。這就是為什麼我們需要衡量聚類效能及其質量的原因。這可以透過輪廓分析來完成。

輪廓分析

此方法可用於透過測量簇之間的距離來檢查聚類的質量。基本上，它提供了一種透過提供輪廓分數來評估引數（如簇數量）的方法。此分數是一個指標，用於衡量一個簇中的每個點與相鄰簇中的點的接近程度。

輪廓分數分析

該分數的範圍為 [-1, 1]。以下是此分數的分析：

• +1 分數 – 接近 +1 的分數表示樣本遠離相鄰簇。

• 0 分數 – 0 分數表示樣本位於或非常靠近兩個相鄰簇之間的決策邊界。

• -1 分數 – 負分數表示樣本已被分配到錯誤的簇中。

計算輪廓分數

在本節中，我們將學習如何計算輪廓分數。

輪廓分數可以使用以下公式計算：

$$silhouette score = \frac{\left ( p-q \right )}{max\left ( p,q \right )}$$

這裡，𝑝 是到資料點不屬於的最近簇中點的平均距離。並且，𝑞 是到其自身簇中所有點的平均簇內距離。

為了找到最佳簇數量，我們需要透過從 sklearn 包中匯入 metrics 模組再次執行聚類演算法。在下面的示例中，我們將執行 K 均值聚類演算法以找到最佳簇數量：

匯入必要的包，如所示：

import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
from sklearn.cluster import KMeans

藉助以下程式碼，我們將使用 sklearn.dataset 包中的 make_blob 生成包含四個斑點的二維資料集。

from sklearn.datasets.samples_generator import make_blobs

X, y_true = make_blobs(n_samples = 500, centers = 4, cluster_std = 0.40, random_state = 0)

初始化變數，如所示：

scores = []
values = np.arange(2, 10)

我們需要遍歷所有值的 K 均值模型，還需要使用輸入資料對其進行訓練。

for num_clusters in values:
kmeans = KMeans(init = 'k-means++', n_clusters = num_clusters, n_init = 10)
kmeans.fit(X)

現在，使用歐幾里得距離度量估計當前聚類模型的輪廓分數：

score = metrics.silhouette_score(X, kmeans.labels_,
metric = 'euclidean', sample_size = len(X))

以下程式碼行將有助於顯示簇數量以及輪廓分數。

print("\nNumber of clusters =", num_clusters)
print("Silhouette score =", score)
scores.append(score)

您將收到以下輸出：

Number of clusters = 9
Silhouette score = 0.340391138371

num_clusters = np.argmax(scores) + values[0]
print('\nOptimal number of clusters =', num_clusters)

現在，最佳簇數量的輸出如下：

Optimal number of clusters = 2

查詢最近鄰

如果我們想構建推薦系統（例如電影推薦系統），那麼我們需要了解查詢最近鄰的概念。這是因為推薦系統利用了最近鄰的概念。

查詢最近鄰的概念可以定義為從給定資料集中查詢最接近輸入點的過程。KNN（K 最近鄰）演算法的主要用途是構建分類系統，這些系統根據輸入資料點與各個類的接近程度對資料點進行分類。

下面給出的 Python 程式碼有助於查詢給定資料集的 K 最近鄰：

匯入必要的包，如下所示。在這裡，我們使用 sklearn 包中的 NearestNeighbors 模組

import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import NearestNeighbors

現在讓我們定義輸入資料：

A = np.array([[3.1, 2.3], [2.3, 4.2], [3.9, 3.5], [3.7, 6.4], [4.8, 1.9], 
             [8.3, 3.1], [5.2, 7.5], [4.8, 4.7], [3.5, 5.1], [4.4, 2.9],])

現在，我們需要定義最近鄰：

k = 3

我們還需要提供要從中查詢最近鄰的測試資料：

test_data = [3.3, 2.9]

以下程式碼可以視覺化並繪製我們定義的輸入資料：

plt.figure()
plt.title('Input data')
plt.scatter(A[:,0], A[:,1], marker = 'o', s = 100, color = 'black')

現在，我們需要構建 K 最近鄰。該物件也需要進行訓練

knn_model = NearestNeighbors(n_neighbors = k, algorithm = 'auto').fit(X)
distances, indices = knn_model.kneighbors([test_data])

現在，我們可以列印 K 個最近鄰，如下所示

print("\nK Nearest Neighbors:")
for rank, index in enumerate(indices[0][:k], start = 1):
   print(str(rank) + " is", A[index])

我們可以將最近鄰與測試資料點一起視覺化

plt.figure()
plt.title('Nearest neighbors')
plt.scatter(A[:, 0], X[:, 1], marker = 'o', s = 100, color = 'k')
plt.scatter(A[indices][0][:][:, 0], A[indices][0][:][:, 1],
   marker = 'o', s = 250, color = 'k', facecolors = 'none')
plt.scatter(test_data[0], test_data[1],
   marker = 'x', s = 100, color = 'k')
plt.show()

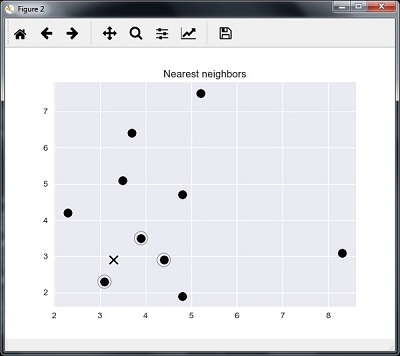
輸出

K 最近鄰

1 is [ 3.1 2.3]
2 is [ 3.9 3.5]
3 is [ 4.4 2.9]

K 最近鄰分類器

K 最近鄰 (KNN) 分類器是一種分類模型，它使用最近鄰演算法對給定資料點進行分類。我們在上一節中實現了 KNN 演算法，現在我們將使用該演算法構建一個 KNN 分類器。

KNN 分類器概念

K近鄰分類的基本概念是找到一個預定義的數字，即“k”個訓練樣本，這些樣本在距離上最接近一個需要分類的新樣本。新樣本將從其鄰居本身獲取標籤。KNN分類器為鄰居的數量設定了一個固定的使用者定義常數，該常數需要確定。對於距離，標準歐氏距離是最常見的選擇。KNN分類器直接作用於學習到的樣本，而不是建立學習規則。KNN演算法是所有機器學習演算法中最簡單的演算法之一。它在大量的分類和迴歸問題中取得了相當大的成功，例如字元識別或影像分析。

示例

我們正在構建一個KNN分類器來識別數字。為此，我們將使用MNIST資料集。我們將在Jupyter Notebook中編寫此程式碼。

匯入如下所示的必要包。

這裡我們使用來自sklearn.neighbors包的KNeighborsClassifier模組 -

from sklearn.datasets import *
import pandas as pd
%matplotlib inline
from sklearn.neighbors import KNeighborsClassifier
import matplotlib.pyplot as plt
import numpy as np

以下程式碼將顯示數字的影像，以驗證我們必須測試哪個影像 -

def Image_display(i):
   plt.imshow(digit['images'][i],cmap = 'Greys_r')
   plt.show()

現在，我們需要載入MNIST資料集。實際上，總共有1797張影像，但我們使用前1600張影像作為訓練樣本，其餘197張將保留用於測試目的。

digit = load_digits()
digit_d = pd.DataFrame(digit['data'][0:1600])

現在，在顯示影像時，我們可以看到如下輸出 -

Image_display(0)

Image_display(0)

數字0的影像顯示如下 -

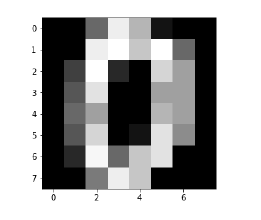
Image_display(9)

數字9的影像顯示如下 -

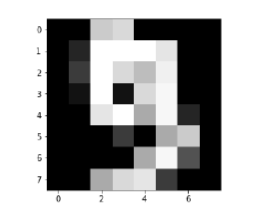
digit.keys()

現在，我們需要建立訓練和測試資料集，並將測試資料集提供給KNN分類器。

train_x = digit['data'][:1600]
train_y = digit['target'][:1600]
KNN = KNeighborsClassifier(20)
KNN.fit(train_x,train_y)

以下輸出將建立K近鄰分類器建構函式 -

KNeighborsClassifier(algorithm = 'auto', leaf_size = 30, metric = 'minkowski',
   metric_params = None, n_jobs = 1, n_neighbors = 20, p = 2,
   weights = 'uniform')

我們需要透過提供任何大於1600的任意數字來建立測試樣本，這些數字是訓練樣本。

test = np.array(digit['data'][1725])
test1 = test.reshape(1,-1)
Image_display(1725)

Image_display(6)

數字6的影像顯示如下 -

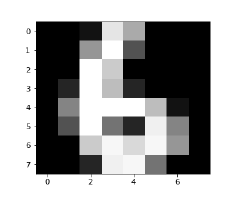
現在我們將預測測試資料，如下所示 -

KNN.predict(test1)

以上程式碼將生成以下輸出 -

array([6])

現在，考慮以下內容 -

digit['target_names']

以上程式碼將生成以下輸出 -

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])