Python AI – 時間序列資料分析

上一頁
下一頁

預測給定輸入序列中的下一個值是機器學習中的另一個重要概念。本章將詳細解釋如何分析時間序列資料。

介紹

時間序列資料是指以特定時間間隔連續出現的資料。如果我們想在機器學習中構建序列預測模型，那麼我們必須處理順序資料和時間。序列資料是順序資料的抽象。資料的順序是順序資料的一個重要特徵。

序列分析或時間序列分析的基本概念

序列分析或時間序列分析是根據先前觀察到的資料來預測給定輸入序列中的下一個值。預測可以是任何可能接下來出現的內容：符號、數字、次日天氣、語音中的下一個詞等等。序列分析在股票市場分析、天氣預報和產品推薦等應用中非常有用。

示例

考慮以下示例來理解序列預測。這裡A,B,C,D是給定的值，您必須使用序列預測模型預測值E。

sequence prediction model

安裝有用的軟體包

對於使用 Python 進行時間序列資料分析，我們需要安裝以下軟體包：

Pandas

Pandas 是一個開源的 BSD 許可庫，它為 Python 提供高效能、易於使用的資料結構和資料分析工具。您可以使用以下命令安裝 Pandas：

pip install pandas

如果您使用的是 Anaconda 並希望使用conda包管理器安裝，則可以使用以下命令：

conda install -c anaconda pandas

hmmlearn

這是一個開源的 BSD 許可庫，它包含簡單的演算法和模型，用於在 Python 中學習隱馬爾可夫模型 (HMM)。您可以使用以下命令安裝它：

pip install hmmlearn

如果您使用的是 Anaconda 並希望使用conda包管理器安裝，則可以使用以下命令：

conda install -c omnia hmmlearn

PyStruct

這是一個結構化學習和預測庫。PyStruct 中實現的學習演算法具有諸如條件隨機場 (CRF)、最大邊際馬爾可夫隨機網路 (M3N) 或結構化支援向量機之類的名稱。您可以使用以下命令安裝它：

pip install pystruct

CVXOPT

它用於基於 Python 程式語言的凸最佳化。它也是一個免費的軟體包。您可以使用以下命令安裝它：

pip install cvxopt

如果您使用的是 Anaconda 並希望使用conda包管理器安裝，則可以使用以下命令：

conda install -c anaconda cvdoxt

Pandas：處理、切片和提取時間序列資料中的統計資訊

如果您需要處理時間序列資料，Pandas 是一個非常有用的工具。藉助 Pandas，您可以執行以下操作：

  • 使用pd.date_range包建立日期範圍

  • 使用pd.Series包按日期索引 Pandas

  • 使用ts.resample包執行重新取樣

  • 更改頻率

示例

以下示例演示瞭如何使用 Pandas 處理和切片時間序列資料。請注意，這裡我們使用的是月度北極濤動資料，可以從monthly.ao.index.b50.current.ascii下載，並可以轉換為文字格式以供我們使用。

處理時間序列資料

要處理時間序列資料，您必須執行以下步驟：

第一步包括匯入以下軟體包：

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

接下來，定義一個函式，該函式將從輸入檔案讀取資料，如下面的程式碼所示：

def read_data(input_file):
   input_data = np.loadtxt(input_file, delimiter = None)

現在，將此資料轉換為時間序列。為此，建立時間序列的日期範圍。在這個示例中，我們將一個月作為資料的頻率。我們的檔案包含從 1950 年 1 月開始的資料。

dates = pd.date_range('1950-01', periods = input_data.shape[0], freq = 'M')

在此步驟中，我們藉助 Pandas Series 建立時間序列資料，如下所示：

output = pd.Series(input_data[:, index], index = dates)	
return output
	
if __name__=='__main__':

在此處輸入輸入檔案的路徑：

input_file = "/Users/admin/AO.txt"

現在，將列轉換為時間序列格式，如下所示：

timeseries = read_data(input_file)

最後，使用顯示的命令繪製和視覺化資料：

plt.figure()
timeseries.plot()
plt.show()

您將觀察到如下所示的圖表：

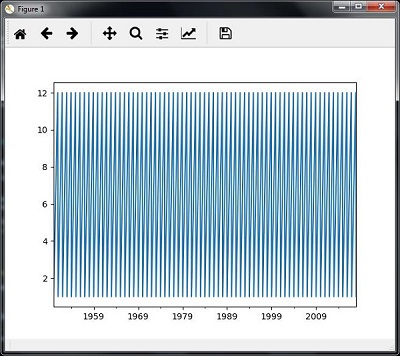
Test Series

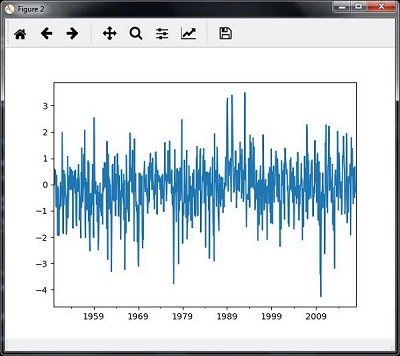
Plots

切片時間序列資料

切片涉及僅檢索時間序列資料的一部分。作為示例的一部分，我們僅從 1980 年到 1990 年切片資料。觀察執行此任務的以下程式碼：

timeseries['1980':'1990'].plot()
   <matplotlib.axes._subplots.AxesSubplot at 0xa0e4b00>

plt.show()

當您執行切片時間序列資料的程式碼時，您可以觀察到此處影像中顯示的圖表：

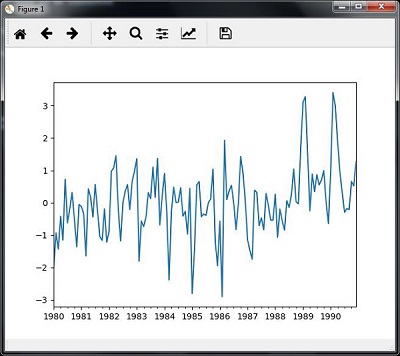
Slicing Time Series Data

從時間序列資料中提取統計資訊

在您需要得出一些重要結論的情況下，您必須從給定資料中提取一些統計資訊。均值、方差、相關性、最大值和最小值就是其中一些統計資訊。如果您想從給定的時間序列資料中提取此類統計資訊，可以使用以下程式碼：

均值

您可以使用mean()函式查詢均值，如下所示：

timeseries.mean()

然後，您將觀察到討論示例的輸出：

-0.11143128165238671

最大值

您可以使用max()函式查詢最大值，如下所示：

timeseries.max()

然後，您將觀察到討論示例的輸出：

3.4952999999999999

最小值

您可以使用 min() 函式查詢最小值，如下所示：

timeseries.min()

然後，您將觀察到討論示例的輸出：

-4.2656999999999998

一次獲取所有內容

如果您想一次計算所有統計資訊，您可以使用describe()函式，如下所示：

timeseries.describe()

然後，您將觀察到討論示例的輸出：

count   817.000000
mean     -0.111431
std       1.003151
min      -4.265700
25%      -0.649430
50%      -0.042744
75%       0.475720
max       3.495300
dtype: float64

重新取樣

您可以將資料重新取樣到不同的時間頻率。執行重新取樣的兩個引數是：

  • 時間段
  • 方法

使用 mean() 進行重新取樣

您可以使用以下程式碼使用 mean() 方法（預設方法）重新取樣資料：

timeseries_mm = timeseries.resample("A").mean()
timeseries_mm.plot(style = 'g--')
plt.show()

然後，您可以觀察到使用 mean() 重新取樣的輸出圖表：

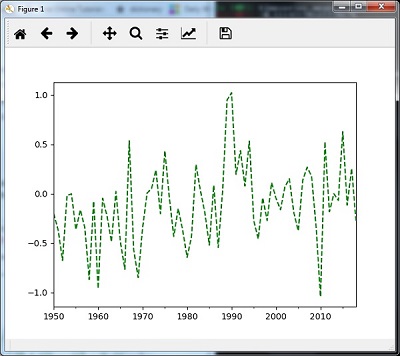
Re Sampling with Mean Method

使用 median() 進行重新取樣

您可以使用以下程式碼使用median()方法重新取樣資料：

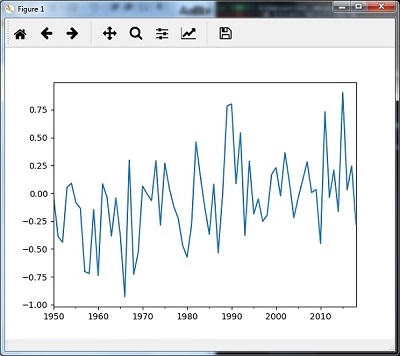
timeseries_mm = timeseries.resample("A").median()
timeseries_mm.plot()
plt.show()

然後，您可以觀察到使用 median() 重新取樣的輸出圖表：

Re Sampling with Median Method

滾動均值

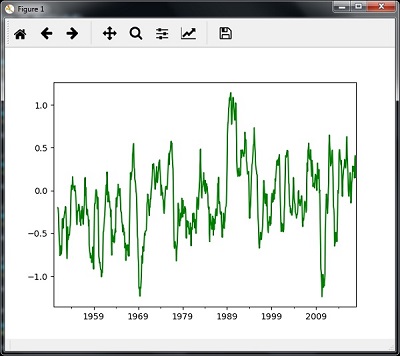
您可以使用以下程式碼計算滾動（移動）均值：

timeseries.rolling(window = 12, center = False).mean().plot(style = '-g')
plt.show()

然後，您可以觀察到滾動（移動）均值的輸出圖表：

Rolling Mean

使用隱馬爾可夫模型 (HMM) 分析順序資料

HMM 是一種統計模型，廣泛用於具有連續性和可擴充套件性的資料，例如時間序列股票市場分析、健康檢查和語音識別。本節詳細介紹了使用隱馬爾可夫模型 (HMM) 分析順序資料。

隱馬爾可夫模型 (HMM)

HMM 是一種隨機模型，它建立在馬爾可夫鏈的概念之上，基於這樣的假設：未來狀態的機率僅取決於當前過程狀態，而不是任何在其之前的狀態。例如，當拋硬幣時，我們不能說第五次拋擲的結果是正面。這是因為硬幣沒有任何記憶，下一個結果不取決於上一個結果。

在數學上，HMM 包含以下變數：

狀態 (S)

它是一組存在於 HMM 中的隱藏狀態或潛在狀態。它表示為 S。

輸出符號 (O)

它是一組存在於 HMM 中的可能輸出符號。它表示為 O。

狀態轉移機率矩陣 (A)

它是從一個狀態轉換到其他每個狀態的機率。它表示為 A。

觀測發射機率矩陣 (B)

它是指在特定狀態下發出/觀察符號的機率。它表示為 B。

先驗機率矩陣 (Π)

它是指從系統的各種狀態開始處於特定狀態的機率。它表示為 Π。

因此，HMM 可以定義為𝝀 = (S,O,A,B,𝝅)，

其中，

  • S = {s1,s2,…,sN}是一組 N 個可能的狀態，
  • O = {o1,o2,…,oM}是一組 M 個可能的觀測符號，
  • A 是一個N𝒙N狀態轉移機率矩陣 (TPM)，
  • B 是一個N𝒙M觀測或發射機率矩陣 (EPM)，
  • π 是一個 N 維初始狀態機率分佈向量。

示例：股票市場資料分析

在這個示例中，我們將逐步分析股票市場資料，以瞭解 HMM 如何與順序資料或時間序列資料一起工作。請注意，我們正在 Python 中實現此示例。

匯入必要的軟體包，如下所示：

import datetime
import warnings

現在，使用matpotlib.finance包中的股票市場資料，如下所示：

import numpy as np
from matplotlib import cm, pyplot as plt
from matplotlib.dates import YearLocator, MonthLocator
try:
   from matplotlib.finance import quotes_historical_yahoo_och1
except ImportError:
   from matplotlib.finance import (
      quotes_historical_yahoo as quotes_historical_yahoo_och1)

from hmmlearn.hmm import GaussianHMM

從開始日期和結束日期載入資料，即在兩個特定日期之間，如下所示：

start_date = datetime.date(1995, 10, 10)
end_date = datetime.date(2015, 4, 25)
quotes = quotes_historical_yahoo_och1('INTC', start_date, end_date)

在此步驟中，我們將提取每天的收盤價。為此，使用以下命令：

closing_quotes = np.array([quote[2] for quote in quotes])

現在，我們將提取每天交易的股票數量。為此，使用以下命令：

volumes = np.array([quote[5] for quote in quotes])[1:]

在這裡，使用以下程式碼獲取收盤價的百分比差異：

diff_percentages = 100.0 * np.diff(closing_quotes) / closing_quotes[:-]
dates = np.array([quote[0] for quote in quotes], dtype = np.int)[1:]
training_data = np.column_stack([diff_percentages, volumes])

在此步驟中，建立並訓練高斯 HMM。為此，使用以下程式碼：

hmm = GaussianHMM(n_components = 7, covariance_type = 'diag', n_iter = 1000)
with warnings.catch_warnings():
   warnings.simplefilter('ignore')
   hmm.fit(training_data)

現在，使用顯示的命令使用 HMM 模型生成資料：

num_samples = 300
samples, _ = hmm.sample(num_samples)

最後，在此步驟中，我們將繪製和視覺化差異百分比和交易的股票數量作為圖表的輸出。

使用以下程式碼繪製和視覺化差異百分比：

plt.figure()
plt.title('Difference percentages')
plt.plot(np.arange(num_samples), samples[:, 0], c = 'black')

使用以下程式碼繪製和視覺化交易的股票數量：

plt.figure()
plt.title('Volume of shares')
plt.plot(np.arange(num_samples), samples[:, 1], c = 'black')
plt.ylim(ymin = 0)
plt.show()
列印頁面
上一篇
下一篇
相關廣告
© . All rights reserved.