資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
服裝學
法學一輛以52千米/小時速度行駛的汽車，駕駛員踩下剎車，並以均勻的加速度向相反方向運動。汽車在5秒內停止。另一輛車以3千米/小時的速度行駛，駕駛員緩慢踩下剎車，並在10秒內停止。在同一張圖紙上，繪製兩輛車的速度-時間圖。哪輛車在踩下剎車後行駛的距離更遠？
已知：一輛汽車以52千米/小時的速度行駛，駕駛員踩下剎車，並以均勻的加速度向相反方向運動。汽車在5秒內停止。另一輛車以3千米/小時的速度行駛，駕駛員緩慢踩下剎車，並在10秒內停止。
要求：在同一張圖紙上繪製兩輛車的速度-時間圖。找出在踩下剎車後行駛距離更遠的汽車。
解題步驟
對於汽車₁
初始速度 u = 52 千米/小時 [已知]
= 52 × 5/18 米/秒 [將千米/小時轉換為米/秒]
= 14.44 米/秒
最終速度 v = 0
時間 t = 5 秒
這裡：
當 t = 0 時，速度 = 14.44 米/秒，我們假設這是點 A(0, 14.44)。
當 t = 5 時，速度 = 0，我們假設這是點 B(5, 0)。
對於汽車₂
初始速度 u = 3 千米/小時 [已知]
= 3 × 5/18 米/秒 [將千米/小時轉換為米/秒]
= 0.83 米/秒
時間 t = 10 秒
最終速度 v = 0
這裡：
當 t = 0 秒時，速度 = 0.83 米/秒，我們假設這是點 C(0, 0.83)
當 t = 10 秒時，速度 = 0，我們假設這是點 D(10, 0)
兩輛車的速度-時間圖：
在座標圖上繪製點 A(0, 14.44) 和 B(5, 0)，我們得到表示汽車₁速度-時間圖的線段 AB。
在座標圖上繪製點 C(0, 0.83) 和 D(10, 0)，我們得到表示汽車₂速度-時間圖的線段 CD。
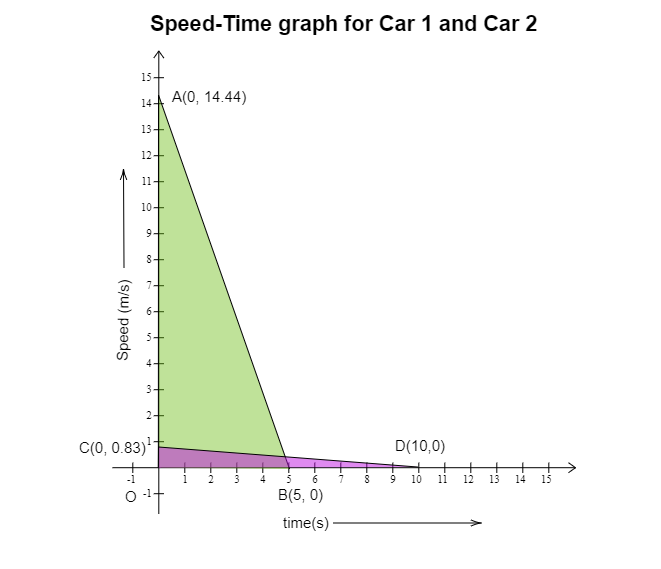
汽車₁行駛的距離 = 三角形 AOB 的面積
= 1/2 × AO × OB
= 1/2 × 14.44 × 5
= 7.22 × 5
= 36.10 米
汽車₂行駛的距離 = 三角形 COD 的面積
= 1/2 × CO × OD
= 1/2 × 0.83 × 10
= 0.41 × 10
= 4.1 米
因此，汽車₁在踩下剎車後行駛的距離更遠。
瀏覽量：153
