資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚學
法律學兩條垂直相交的十字路口，每條路口寬 10 m，穿過一個矩形公園的中心，該公園長 700 m，寬 300 m，並平行於其邊。求路口的面積。還要找出不包括十字路口的公園面積。以公頃為單位給出答案。
從問題中，已知
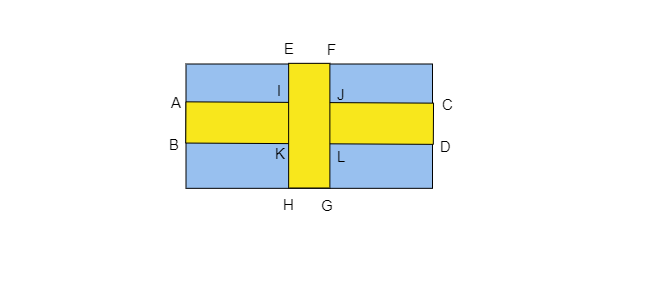
公園長度 $(L) = 700\ m$
公園寬度 $(B) = 300\ m$
那麼
公園面積 $= 長度\times 寬度$
$= 700\times 300$
$= 210000\ m^2$
我們假設 ABCD 是公園中的一個十字路口，EFGH 是另一個十字路口。
ABCD 十字路口的長度 $= 700\ m$
EFGH 十字路口的長度 $= 300\ m$
兩個十字路口的寬度相同 $= 10\ m$
那麼
ABCD 十字路口的面積 $= 長度\times 寬度$
$= 700\times 10$
$= 7000\ m^2$
EFGH 十字路口的面積 $= 長度\times 寬度$
$= 300\times 10$
$= 3000\ m^2$
中心 $IJKL$ 的面積$= 長度\times 寬度$
$= 10\times 10$
$= 100\ m^2$
道路的面積 $=$ $ABCD$ 的面積 +$ EFGH$ 的面積 -$ IJKL$ 的面積
$= 7000 + 3000 – 100$
$= 10000 – 100$
$= 9900\ m^2$
我們知道對於 $1公頃 = 10000\ m^2$
因此，道路面積公頃 $= \frac{9900}{10000}$
$= 0.99公頃$
最後，不包括道路的公園面積 $=$ 公園面積 $-$ 道路面積
$= 210000-9900$
$= 200100\ m^2$
$= \frac{200100}{10000}$
$= 20.01公頃$
更新於: 10-Oct-2022
61 次瀏覽
廣告