資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究C++ 無向圖中所有連通分量的最小元素之和
在這個問題中，我們得到一個包含 N 個數字的陣列 arr，其中 arr[i] 代表第 (i+1) 個節點。此外，還有 M 對邊，其中 u 和 v 代表由邊連線的節點。我們的任務是建立一個程式來查詢無向圖中所有連通分量的最小元素之和。如果一個節點與任何其他節點都沒有連線，則將其計為只有一個節點的連通分量。
讓我們來看一個例子來理解這個問題：
輸入
arr[] = {2, 7, 5, 1, 2} m = 2
1 2
4 5輸出
8
解釋
以下是上面描述的圖：
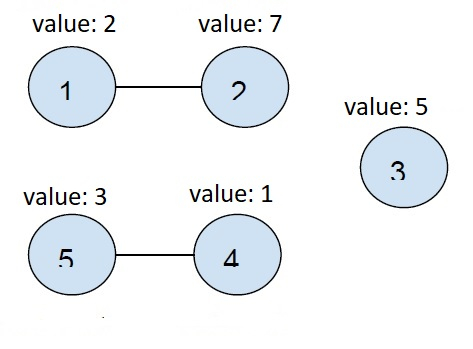
我們有兩個連線的節點和一個單個節點。
因此，讓我們取所有連通分量的最小值。
Min (節點1 和 節點2) = min (2, 7) = 2
Min (節點4 和 節點5) = min (1, 3) = 1
Min (節點3) = min (5) = 5
總和 = 1 + 2 + 5 = 8
為了解決這個問題，我們將使用任何遍歷技術（BFS 或 DFS）查詢無向圖的所有連通節點，然後為所有已訪問的節點建立一個已訪問陣列，以避免重複訪問。在訪問直接或間接連線的連通節點時，我們將找到所有連線的最小值。並將此最小值新增到 sum 變數中。訪問所有節點後，我們將列印 sum。
示例
程式演示了我們解決方案的工作原理：
#include <bits/stdc++.h>
using namespace std;
const int N = 100;
vector<int> graph[N];
bool visited[N];
void dfs(int node, int arr[], int minimum){
minimum = min(minimum, arr[node]);
visited[node] = true;
for (int i : graph[node]) {
if (!visited[i])
dfs(i, arr, minimum);
}
}
void createEdge(int u, int v){
graph[u - 1].push_back(v - 1);
graph[v - 1].push_back(u - 1);
}
int minSum(int arr[], int n){
int sum = 0;
for (int i = 0; i < n; i++) {
if (!visited[i]) {
int minimum = arr[i];
dfs(i, arr, minimum);
sum += minimum;
}
}
return sum;
}
int main(){
int arr[] = {2, 7, 5, 1, 3};
createEdge(1, 2);
createEdge(4, 5);
int n = sizeof(arr) / sizeof(arr[0]);
cout<<"The sum of minimum elements in all connected components of an undirected graph is ";
cout<<minSum(arr, n);
return 0;
}輸出
The sum of minimum elements in all connected components of an undirected graph is 8
更新於：2020年8月6日
361 次檢視
廣告