資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究用 C++ 列印無向圖中的所有環
在這個問題中，我們給定一個無向圖，我們需要列印圖中形成的所有環。
無向圖是一個相互連線的圖。無向圖的所有邊都是雙向的。它也稱為無向網路。
圖資料結構中的環是指所有頂點都形成一個環的圖。
讓我們看一個例子來更好地理解這個問題 -
圖 -
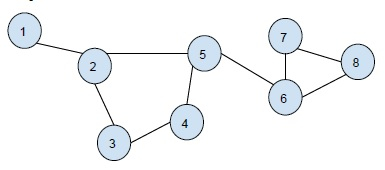
輸出 -
Cycle 1: 2 3 4 5 Cycle 2: 6 7 8
為此，我們將利用圖的一些特性。您需要使用圖著色方法並對出現在迴圈圖中的所有頂點進行著色。此外，如果一個頂點被部分訪問，它將導致一個迴圈圖。因此，我們將對這個頂點和所有後續頂點進行著色，直到再次到達相同的頂點。
演算法
Step 1: call DFS traversal for the graph which can color the vertices. Step 2: If a partially visited vertex is found, backtrack till the vertex is reached again and mark all vertices in the path with a counter which is cycle number. Step 3: After completion of traversal, iterate for cyclic edge and push them into a separate adjacency list. Step 4: Print the cycles number wise from the adjacency list.
示例
#include <bits/stdc++.h>
using namespace std;
const int N = 100000;
vector<int> graph[N];
vector<int> cycles[N];
void DFSCycle(int u, int p, int color[], int mark[], int par[], int& cyclenumber){
if (color[u] == 2) {
return;
}
if (color[u] == 1) {
cyclenumber++;
int cur = p;
mark[cur] = cyclenumber;
while (cur != u) {
cur = par[cur];
mark[cur] = cyclenumber;
}
return;
}
par[u] = p;
color[u] = 1;
for (int v : graph[u]) {
if (v == par[u]) {
continue;
}
DFSCycle(v, u, color, mark, par, cyclenumber);
}
color[u] = 2;
}
void insert(int u, int v){
graph[u].push_back(v);
graph[v].push_back(u);
}
void printCycles(int edges, int mark[], int& cyclenumber){
for (int i = 1; i <= edges; i++) {
if (mark[i] != 0)
cycles[mark[i]].push_back(i);
}
for (int i = 1; i <= cyclenumber; i++) {
cout << "Cycle " << i << ": ";
for (int x : cycles[i])
cout << x << " ";
cout << endl;
}
}
int main(){
insert(1, 2);
insert(2, 3);
insert(3, 4);
insert(4, 5);
insert(5, 2);
insert(5, 6);
insert(6, 7);
insert(7, 8);
insert(6, 8);
int color[N];
int par[N];
int mark[N];
int cyclenumber = 0;
cout<<"Cycles in the Graph are :\n";
int edges = 13;
DFSCycle(1, 0, color, mark, par, cyclenumber);
printCycles(edges, mark, cyclenumber);
}輸出
圖中的環 -
Cycle 1: 2 3 4 5 Cycle 2: 6 7 8
更新於: 2020年1月17日
2K+ 次瀏覽
廣告