資料結構
網路
RDBMS
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英文
經濟學
心理學
社會科學
時尚
法律檢測無向圖中的環
要檢測無向圖中是否存在環，我們應該對給定的圖使用 DFS 遍歷。對於每個訪問過的頂點 v，當我們找到任何相鄰頂點 u 時，u 已被訪問，並且 u 不是頂點 v 的父級。那麼將檢測到一個環。
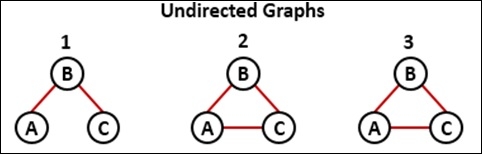
我們假設對於任何一對頂點，沒有平行邊。
Input and Output: Adjacency matrix 0 1 0 0 0 1 0 1 1 0 0 1 0 0 1 0 1 0 0 1 0 0 1 1 0 Output: The graph has cycle.
演算法
dfs(vertex, visited, parent)
Input: The start vertex, the visited set, and the parent node of the vertex.
Output: True a cycle is found.Begin add vertex in the visited set for all vertex v which is adjacent with vertex, do if v = parent, then return true if v is not in the visited set, then return true if dfs(v, visited, vertex) is true, then return true done return false End hasCycle(graph) Input: The given graph. Output: True when a cycle has found.Begin for all vertex v in the graph, do if v is not in the visited set, then go for next iteration if dfs(v, visited, φ) is true, then //parent of v is null return true return false done End
示例
#include<iostream>
#include<set>
#define NODE 5
using namespace std;
int graph[NODE][NODE] = {
{0, 1, 0, 0, 0},
{1, 0, 1, 1, 0},
{0, 1, 0, 0, 1},
{0, 1, 0, 0, 1},
{0, 0, 1, 1, 0}
};
bool dfs(int vertex, set<int>&visited, int parent) {
visited.insert(vertex);
for(int v = 0; v<NODE; v++) {
if(graph[vertex][v]) {
if(v == parent) //if v is the parent not move that direction
continue;
if(visited.find(v) != visited.end()) //if v is already visited
return true;
if(dfs(v, visited, vertex))
return true;
}
}
return false;
}
bool hasCycle() {
set<int> visited; //visited set
for(int v = 0; v<NODE; v++) {
if(visited.find(v) != visited.end()) //when visited holds v, jump to next iteration
continue;
if(dfs(v, visited, -1)) { //-1 as no parent of starting vertex
return true;
}
}
return false;
}
int main() {
bool res;
res = hasCycle();
if(res)
cout << "The graph has cycle." << endl;
else
cout << "The graph has no cycle." << endl;
}輸出
The graph has cycle.
更新時間：16-Jun-2020
7K+ 瀏覽
廣告