資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法學檢查無向圖中節點 S 和 T 之間是否存在僅 S 和 T 重複的環路
介紹
圖是一種強大的數學結構，允許我們對各種實體之間的關係進行建模和視覺化。在計算機科學中，圖在各種演算法和資料結構中都有應用。無向圖的一個常見問題是確定兩個給定節點之間是否存在環路。在本文中，我們將著手解決這個難題，並使用 C/C++ 提供一個優雅的解決方案。確定無向圖中的環路對於各種連線性很重要的應用至關重要。
無向圖是確定兩個給定節點之間是否存在環路
無權雙向（或無向）圖由透過邊連線的頂點或節點組成。這些邊沒有分配任何特定的權重或距離，而是僅指示存在連線，沒有任何方向偏差。
路徑表示一系列互連的頂點，其中每個頂點都透過邊直接與其相鄰的對應頂點連線。在這裡，我們專注於查詢連線兩個不同頂點（明確稱為源節點和目標節點）的路徑，並具有最小的總邊遍歷次數。
考慮一個無向圖，其中每條邊表示兩個節點之間的連線。我們的目標是確定在這個圖中是否存在連線節點 S 和節點 T 的環路，當這兩個節點都可以在任何路徑中重複出現。
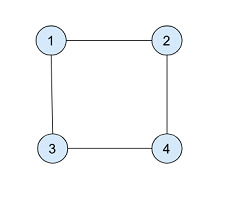
在上圖中，它有四個頂點和 3 條邊，我們需要檢查節點 1 和節點 4 之間是否存在環路。DFS 演算法從節點 1（源節點）開始，訪問其相鄰節點 - 節點 2 和節點 3。然後它訪問節點 4，該節點之前已被節點 3 訪問過。由於節點 4 不是節點 3 的父節點，因此圖中存在環路。
方法 1：C++ 程式，用於檢查無向圖中節點 S 和 T 之間是否存在僅 S 和 T 重複的環路
為了有效地解決這個問題，我們將採用深度優先搜尋 (DFS)，這是一種廣泛使用的圖遍歷演算法。DFS 背後的基本思想是儘可能沿著每個分支向下探索，然後再回溯。
演算法
步驟 1 − 它使用一個 `Graph` 類來封裝圖的屬性。
步驟 2 − 它包括諸如 `addEdge()`（連線兩個頂點）、`hasCycle()`（確定兩個節點之間是否存在環路）以及用於 DFS 遍歷的內部輔助方法（例如 `dfsUtil()`）之類的函式。
步驟 3 − 在驅動程式程式碼 (`main()` )中，我們提示使用者輸入圖中的頂點數和邊數。
步驟 4 − 然後逐一詢問邊對（節點連線）。
步驟 5 − 最後，詢問源頂點和目標頂點。
步驟 6 − 程式將輸出這兩個節點之間是否存在可能重複的路徑。
示例
#include <iostream>
#include <vector>
using namespace std;
// Graph class representing our underlying structure
class Graph {
int numNodes; // Total number of nodes in the graph
vector<vector<int>> adjList; // Adjacency list representation
public:
// Constructor taking input parameter specifying the total number of nodes
Graph(int n) {
numNodes = n;
adjList.resize(n);
}
// Function allowing adding edges between two vertices u and v (0-based indexing)
void addEdge(int u, int v) {
adjList[u].push_back(v);
adjList[v].push_back(u);
}
private:
// Utility function used by hasCycle() to perform DFS search recursively starting from vertex s.
// It returns true if the cycle is found during exploration.
bool dfsUtil(int s, bool visited[], bool parent[]) {
visited[s] = true;
for (int v : adjList[s]) {
if (!visited[v]) {
parent[v] = true;
// Recursive call
if (dfsUtil(v, visited, parent))
return true;
}
else if(parent[v])
return true;
}
return false;
}
public:
// Function that checks whether a cycle exists between nodes S and T.
bool hasCycle(int s, int t) {
bool* visited = new bool[numNodes];
bool* parent = new bool[numNodes];
for(int i=0; i<numNodes; ++i){
visited[i]=false;
parent[i]=false;
}
parent[s] = true;
if(dfsUtil(s, visited, parent)){
delete[] visited;
delete[] parent;
return dfsUtil(t,visited,parent);
}
delete[] visited;
return false;
}
};
int main() {
int numVertices = 4;
int numEdges = 4;
Graph graph(numVertices);
vector<pair<int,int>> edges = {{1,2},{2,3},{3,4},{4,1}};
for(auto edge : edges){
int u = edge.first - 1;
int v = edge.second - 1;
graph.addEdge(u,v);
}
int source = 1 - 1;
int target = 4 - 1;
if(graph.hasCycle(source,target))
cout<<"A cycle exists between node "<< source+1 <<" and node " <<target+1<<".";
else
cout<<"No cycle found between node "<< source+1<<" and node " <<target + 1<<".";
return 0;
}
輸出
A cycle exists between node 1 and node 4.
結論
當可以透過在不同路徑上重複特定節點來形成環路時，這個問題變得更加有趣。透過利用深度優先搜尋 (DFS)，我們已經成功開發出健壯的 C++ 程式碼，該程式碼包含用於探索圖的解決方案，同時有效地檢查連線所選節點 S 和 T 的重複項的環路是否存在。
94 次瀏覽
