資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究在 C++ 中查詢流網路中的最小 s-t 割
假設我們有以下流網路。眾所周知，s-t 割是指將源節點 s 和匯點 t 分到不同子集中所需的割，並且它包含從源集到匯點側的邊。此處，s-t 割的容量由割集中每條邊的容量之和表示。在這裡，我們必須找到給定網路的最小容量 s-t 割。此處，預期輸出是最小割的所有邊。
因此，如果輸入類似於
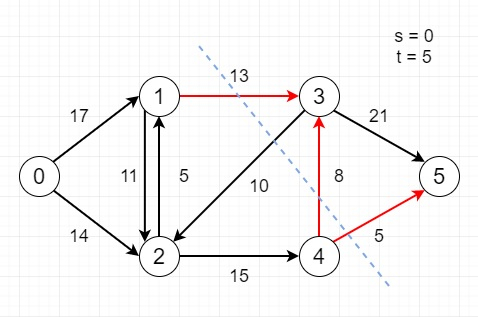
則輸出將為 [(1,3), (4,3), (4,5)]
為了解決這個問題，我們將遵循以下步驟：
節點數 NODES = 6
定義一個函式 bfs()，它將接收圖、源節點 src、匯點 sink 和陣列 par 作為引數。
定義一個大小為 NODES 的陣列 vis，並將其全部填充為 0。
定義一個佇列 que。
將源節點 src 插入佇列 que 中。
將 vis[src] 設定為 true，並將 par[src] 設定為 -1。
當 (佇列 que 不為空) 時，執行以下操作：
u1 := 佇列 que 的第一個元素。
從佇列 que 中刪除該元素。
初始化 v1 := 0，當 v1 < NODES 時，更新 (將 v1 增加 1)，執行以下操作：
如果 vis[v1] 為假且 graph[u1, v1] > 0，則執行以下操作：
將 v1 插入佇列 que 中。
par[v1] := u1。
vis[v1] := true。
當 vis[sink] 為真時，返回 true。
定義一個函式 dfs()，它將接收圖、源節點 src 和陣列 vis 作為引數。
vis[src] := true。
初始化 i := 0，當 i < NODES 時，更新 (將 i 增加 1)，執行以下操作：
如果 graph[src, i] 不為零且 vis[i] 為假，則執行以下操作：
dfs(graph, i, vis)。
從主方法中，執行以下操作：
定義一個數組 temp_graph 並將 graph 複製到其中。
定義一個大小為 NODES 的陣列 par。
當 bfs(temp_graph, src, sink, par) 為真時，執行以下操作：
path_flow := 無窮大。
初始化 v := sink，當 v 不等於 src 時，更新 v:=par[v]，執行以下操作：
u := par[v]。
path_flow := path_flow 和 temp_graph[u, v] 中的最小值。
初始化 v := sink，當 v 不等於 src 時，更新 v:=par[v]，執行以下操作：
u := par[v]。
temp_graph[u, v] := temp_graph[u, v] - path_flow。
temp_graph[v, u] := temp_graph[v, u] + path_flow。
定義一個大小為 NODES 的陣列 vis，並將其全部填充為 false。
dfs(temp_graph, src, vis)。
初始化 i := 0，當 i − NODES 時，更新 (將 i 增加 1)，執行以下操作：
初始化 j := 0，當 j − NODES 時，更新 (將 j 增加 1)，執行以下操作：
如果 vis[i] 不為零且 vis[j] 為假且 graph[i, j] 不為零，則執行以下操作：
顯示 (i, j) 作為邊。
返回。
示例 (C++)
讓我們看看以下實現以更好地理解：
#include <bits/stdc++.h>
using namespace std;
#define NODES 6
int bfs(int graph[NODES][NODES], int src, int sink, int par[]) {
bool vis[NODES];
memset(vis, 0, sizeof(vis));
queue <int> que;
que.push(src);
vis[src] = true;
par[src] = -1;
while (!que.empty()) {
int u1 = que.front();
que.pop();
for (int v1=0; v1<NODES; v1++){
if (vis[v1]==false && graph[u1][v1] > 0) {
que.push(v1);
par[v1] = u1;
vis[v1] = true;
}
}
}
return (vis[sink] == true);
}
void dfs(int graph[NODES][NODES], int src, bool vis[]) {
vis[src] = true;
for (int i = 0; i < NODES; i++)
if (graph[src][i] && !vis[i])
dfs(graph, i, vis);
}
void minCut(int graph[NODES][NODES], int src, int sink) {
int u, v;
int temp_graph[NODES][NODES];
for (u = 0; u < NODES; u++)
for (v = 0; v < NODES; v++)
temp_graph[u][v] = graph[u][v];
int par[NODES];
while (bfs(temp_graph, src, sink, par)){
int path_flow = INT_MAX;
for (v=sink; v!=src; v=par[v]) {
u = par[v];
path_flow = min(path_flow, temp_graph[u][v]);
}
for (v=sink; v != src; v=par[v]) {
u = par[v];
temp_graph[u][v] -= path_flow;
temp_graph[v][u] += path_flow;
}
}
bool vis[NODES];
memset(vis, false, sizeof(vis));
dfs(temp_graph, src, vis);
for (int i = 0; i < NODES; i++)
for (int j = 0; j < NODES; j++)
if (vis[i] && !vis[j] && graph[i][j])
cout << "("<< i << ", " << j << ")" << endl;
return;
}
int main() {
int graph1[NODES][NODES] = {
{0, 17, 14, 0, 0, 0},
{0, 0, 11, 13, 0, 0},
{0, 5, 0, 0, 15, 0},
{0, 0, 9, 0, 0, 21},
{0, 0, 0, 8, 0, 5},
{0, 0, 0, 0, 0, 0}
};
minCut(graph1, 0, 5);
}輸入
{{0, 17, 14, 0, 0, 0},
{0, 0, 11, 13, 0, 0},
{0, 5, 0, 0, 15, 0},
{0, 0, 9, 0, 0, 21
{0, 0, 0, 8, 0, 5},
{0, 0, 0, 0, 0, 0}};輸出
(1, 3) (4, 3) (4, 5)
259 次瀏覽
