資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究Python程式：查詢切割木棍的最小成本
假設我們有一個值n和一個名為cuts的陣列。考慮一根長度為n個單位的木棍。木棍從0到n標記。這裡cuts[i]表示我們可以切割的位置。我們應該按順序執行切割，但是我們可以根據需要更改切割的順序。這裡一次切割的成本是待切割木棍的大小，總成本是所有切割成本的總和。我們必須找到切割的最小總成本。
因此，如果輸入類似於n = 7，cuts = [5,1,4,3]，則輸出將為16，因為如果我們按[3,5,1,4]的順序排列它們，則首先從長度為7的木棍上切割3，所以成本為7，然後我們有兩部分長度為3和4，然後切割5，所以成本為4，到目前為止總成本為7+4=11，然後從木棍大小為2的地方切割4，所以總成本為7+4+2 = 13，最後切割3，所以成本為3，最終成本為7+4+2+3 = 16。
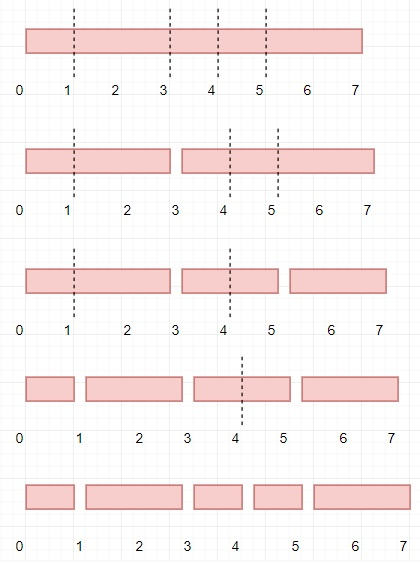
為了解決這個問題，我們將遵循以下步驟：
cuts := 一個列表，其中cuts中的元素按排序順序排列，並在開頭插入0並在結尾插入n
m := cuts的大小
cost := 建立一個大小為m x m的方陣並填充0
對於k從2到m - 1，執行
對於i從0到m - 1，執行
j := i + k
如果j >= m，則
進入下一次迭代
cost[i, j] = (cuts[j] - cuts[i]) + (cost[i, s] + cost[s, j] 在所有s在range(i+1, j-1)中的最小值)
返回cost[0, m-1]
示例
讓我們看看下面的實現以更好地理解
def solve(n, cuts): cuts = [0] + sorted(cuts) + [n] m = len(cuts) cost = [[0]*m for _ in range(m)] for k in range(2, m): for i in range(m): j = i + k if j >= m: continue cost[i][j] = (cuts[j]-cuts[i]) + min(cost[i][s] + cost[s][j] for s in range(i+1, j)) return cost[0][m-1] n = 7 cuts = [5,1,4,3] print(solve(n, cuts))
輸入
7, [5,1,4,3]
輸出
16
更新於：2021年10月6日
693 次瀏覽
廣告