無向圖中簡單環的數量 (N個頂點)

---

引言

無向圖是計算機科學和圖論中的一個重要組成部分，它表示一組由邊連線的節點，這些邊沒有方向性。與無向圖相關的常見問題之一是計算簡單環或迴路的數量，簡單環是指僅訪問每個頂點一次的閉合路徑。在本文中，我們將探討如何使用功能強大的程式語言C和C++來計算具有N個頂點的給定無向圖中簡單環的總數。

無向圖

在我們開始編碼之前，讓我們確保每個人都理解無向圖中簡單環的構成。

讓我們考慮一個具有四個頂點（N=4）的無向圖，如下所示：

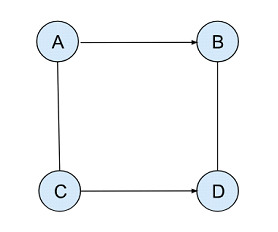
在這個例子中，每個簡單環都從一個頂點開始，並以同一個頂點結束，訪問所有四個頂點，同時確保每個節點只訪問一次。

圖的表示

首先，為我們的圖建立一個合適的表示至關重要。最常用的方法是使用鄰接表或鄰接矩陣。

• 鄰接表 - 每個節點儲存與其相鄰節點的連線。

• 鄰接矩陣 - 使用一個方陣，其中行和列表示頂點，填充的值表示邊的連線。

深度優先搜尋 (DFS)

下一步是對我們的圖進行深度優先搜尋，從每個可能的頂點開始，如下所示：

• 遞迴地訪問每個未訪問的相鄰頂點，直到到達一個先前訪問過的節點（環的閉合）。

• 為了區分同時探索的不同路徑，在DFS遍歷期間標記已訪問的節點。

• 在DFS實現過程中跟蹤所有遇到的唯一環，以便進一步分析。

計算簡單環

為了有效地獲得整個圖的準確計數，需要結合以下要素：

• 從每個頂點分別執行DFS，並使用布林陣列維護先前訪問過的節點的資訊。

• 在每次遞迴呼叫期間跟蹤路徑，並維護一個已訪問節點列表以檢測環的形成。

• 透過附加初始頂點來儲存每個發現的環，以建立一個完整的迴圈。

C++程式：計算具有N個頂點的給定無向圖中的簡單環數量

簡單環的數量使用給定鄰接矩陣中的遞迴函式計算。

演算法

• 步驟1 - 使用包含C++中所有函式的全包標頭檔案。

• 步驟2 - “V”變數用整數資料型別初始化。

• 步驟3 - 已訪問的頂點表示為“vis”，它包含布林陣列以獲取環的數量。

• 步驟4 - 使用的圖是動態規劃，它是一個函式，它採用三個引數作為起始頂點、當前頂點和環的長度。

• 步驟5 - 假設當前頂點已被訪問，for迴圈將遍歷鄰接矩陣值的每個節點。

• 步驟6 - 當下一個頂點是起始頂點時，計數將遞增。

• 步驟7 - 根據矩陣值，將返回無向圖計數。

示例

//using the required header files which includes all the header within it
#include <bits/stdc++.h> 
using namespace std;

// Adjacency matrix is represented in an array
void Vertex(int V, vector<vector<int> > graph) {
   // Declaring the variable count with a value of 0
   int count = 0;
   int dp[(1 << V)][V];

   // Declaring with a value of 0
   memset(dp, 0, sizeof dp);

   // for loop will iterate through 
   for (int num = 0;
      num < (1 << V); num++) {

         // To get the number of bits
         int nodes
         = __builtin_popcountll(num);
         // To find the first bit
         int first
         = __builtin_ffsl(num);
		
         if (nodes == 1) {

            // Declaring with a value of 1
            dp[num][first] = 1;
         } else {

            // Resetting visited array before each traversal
            // Dynamic programming starts from vertex i where the current cycle has only one node and increments the value by 1
            for (int val = first + 1;
               val < V; val ++) {
				
            if ((num & (1 << val))) {
					
               int newnum = num ^ (1 << val);
   
               for (int k = 0; k < V; k++) {

                  if ((newnum & (1 << k)) && graph[k][val]) {
                     dp[num][val]
                     += dp[newnum][k];

                     //Graph connected to the first node
                     if (graph[val][first] && nodes > 2)
                        count += dp[num][val];
                  }
               }
            }
         }
      }
   }

   // Getting the final answer
   cout << count << endl;
}

// main function
int main() {
   // In the graph, the vertices in initialized with a value of 4
   int V = 4; 
  
   // Declaring the input as adjacency matrix
   vector<vector<int> > graph = { { 1, 1, 1, 1 }, 
      { 1, 0, 1, 1 }, 
      { 1, 1, 0, 1 }, 
      { 1, 1, 1, 0 } };

   Vertex(V, graph);

   return 0;
}

輸出

2

結論

透過本文中的詳細描述以及提供的C++實現示例，我們現在可以解決涉及計算簡單環的類似問題。在處理各種具有挑戰性的問題時，計算給定圖中的環至關重要。透過使用深度優先搜尋和適當的資料結構來有效地描述圖，可以進行此類計算。