1 到 25 的平方根

---

簡介

1 到 25 的平方根是 1 到 25 所有數字的平方根列表。平方根可以具有不同型別的數值。1 到 25 的根的正整數數值範圍從 1 到 5。對於非完全平方數，平方根是一個無理數。

任何數字 x 的根表示為 √𝑥（根式）和 $\mathrm{(x)^{2}}$（指數式）

平方根

任何數字的平方根是可以乘以自身得到原數字的值。平方根是平方數的逆運算。因此，平方和平方根是相關的概念。

如果 x 是 y 的平方根，則表示為 $\mathrm{x\:=\:\sqrt{y}}$。或者，您也可以將原始方程式寫成 $\mathrm{x^{2}\:=\:\sqrt{y}}$。這裡，“√”是用於表示數字平方根的符號（根式）。將一個數字乘以自身得到該數字的平方。有效範圍內的平方數的平方根表示唯一的數字。

例如，三的平方是 9，$\mathrm{3^{2}\:=\:9}$，9 的平方根是 √ 9 = 3。由於 9 是一個完全平方數，因此您可以輕鬆找到平方根。但是對於 3、7、5 等非完全平方數，您必須使用其他方法來找到平方根。

1-25 平方根表

1-25 數字的平方根值的表格為

數字 (x)	數字的平方根 $\mathrm{(\sqrt{X})}$（四捨五入到小數點後 3 位）
1	1.000
2	1.414
3	1.732
4	2.000
5	2.236
6	2.449
7	2.646
8	2.828
9	3.000
10	3.162
11	3.317
12	3.464
13	3.606
14	3.742
15	3.873
16	4.000
17	4.123
18	4.243
19	4.359
20	4.472
21	4.583
22	4.690
23	4.796
24	4.899
25	5.000

求平方根的方法

• 方法 1 - 素因數分解

示例 - $\mathrm{\sqrt{25}}$

25 的素因數分解是 $\mathrm{5\times\:5}$

出現兩次的數字 - 5

因此，$\mathrm{\sqrt{25}\:=\:5}$

• 方法 2 - 長除法

因式分解

完全平方數的平方根可以使用上面詳細討論的因式分解方法輕鬆計算。讓我們在這裡澄清一些示例 -

數字	素因數分解	平方根
16	$\mathrm{2\times\:2\times\:2\times\:2}$	$\mathrm{\sqrt{16}\:=\:2\times\:2\:=\:4}$
144	$\mathrm{2\times\:2\times\:2\times\:2\times\:3\times\:3}$	$\mathrm{\sqrt{144}\:=\:2\times\:2\times\:3\:=\:12}$
169	$\mathrm{13\times\:13}$	$\mathrm{\sqrt{169}\:=\:13}$
256	$\mathrm{256\:=\:2\times\:2\times\:2\times\:2\times\:2\times\:2\times\:2\times\:2}$	$\mathrm{\sqrt{256}\:=\:(2\times\:2\times\:2\times\:2)\:=\:16}$
576	$\mathrm{576\:=\:2\times\:2\times\:2\times\:2\times\:2\times\:2\times\:3\times\:3}$	$\mathrm{\sqrt{576}\:=\:2\times\:2\times\:2\times\:3\:=\:24}$

估計

此方法用作近似值來猜測數值並找到平方根。

例如，4 的平方根是 2，9 的平方根是 3，因此我們可以推斷 5 的平方根介於 2 和 3 之間

但是您需要檢視 $\mathrm{\sqrt{5}}$ 的數值是接近 2 還是 3。

讓我們檢查 2.2 和 2.8 的平方。

$\mathrm{2.2\:=\:4.84}$

$\mathrm{2.8\:=\:7.84}$

由於 2.2 的平方根更接近 5，因此我們可以估計 5 的平方根約等於 2.2

長除法

求非完全平方數的平方根有點困難，但是可以使用稱為長除法的方法計算。這可以透過下面的示例來理解

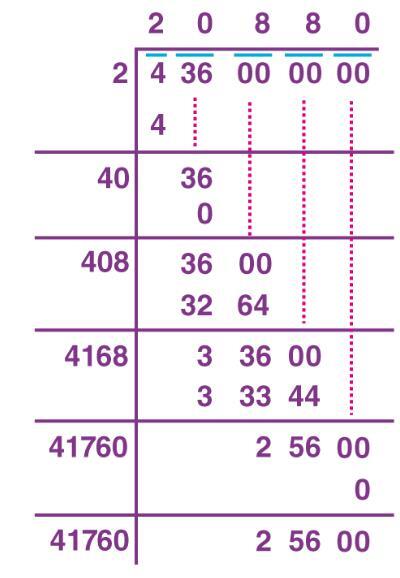
已解決示例

1)正方形金屬板的面積為 18 平方英寸。求該金屬板一邊的尺寸。

答案 -

設金屬板的一邊尺寸為“a”

正方形金屬板面積 $\mathrm{=\:18\:in^{2}\:=\:a^{2}}$

$$\mathrm{即\:a^{2}\:=\:18}$$

$$\mathrm{a\:=\:\sqrt{18}\:=\:4.243\:in}$$

因此，金屬板邊長為 4.243 英寸

2)一個圓形桌面，面積為 19π 平方英寸。求桌面的半徑（以英寸為單位）？

答案 -

圓形桌面面積 $\mathrm{=\:19\pi\:in^{2}\:=\:\pi\:r^{2}}$

即 $\mathrm{19\:=\:r^{2}}$ 2。因此，使用半徑中的數值 $\mathrm{=\:\sqrt{19}}$

桌面半徑 = 4.359 英寸。

3) 求 $\mathrm{6\sqrt{7}\:+\:3\sqrt{7}}$ 的值

答案 -

$\mathrm{6\sqrt{7}\:+\:3\sqrt{7}\:=\:6\times\:(2.646)\:+\:3\:\times\:(2.646)\:=\:9\:\times\:2.646[√7的值為\:2.646]}$

因此 $\mathrm{6\sqrt{7}\:+\:3\sqrt{7}\:=\:9\:\times\:2.646\:=\:23.814}$

結論

在本教程中，我們學習了平方和平方根，主要是 1 到 25 的整數平方根。如果一個數字的範圍具有完全平方數，則該範圍內存在完全平方根。如果數字以偶數個零 (0) 結尾，則它可以有平方根。

您可以將兩個平方根的數值相乘。例如，將 $\mathrm{\sqrt{3}}$ 乘以 $\mathrm{\sqrt{2}}$ 會得到 $\mathrm{\sqrt{6}}$。將兩個相等的平方根相乘，最終結果是初始數字。這意味著結果不再是平方根。例如，將 $\mathrm{\sqrt{7}}$ 乘以 $\mathrm{\sqrt{7}}$ 會得到 7。無理數的平方根是無理數。完全平方數不能為負數。

常見問題解答

1. 1 到 25 的平方根的值是多少？

1 到 25 的平方根值是數字 𝑥，當它乘以自身時會得到原數字。

它可以具有不同型別的數值（正數、負數）。在 1 和 25 之間，1、4、9、16 和 25 的平方根是整數（有理數），而 2、3、5、6、7、8、10、11、12、13、14、15、17、18、19、20、21、22、23 和 24 的平方根是（無理）小數，這些小數不會停止或重複。

2. 如何計算 1 到 25 的平方根？

通常有兩種方法可以計算 1 到 25 的平方根值。素因數分解可用於完全平方數（1、4、9、16 和 25），對於非完全平方數（2、3、5、6、7、8、10、11、12、13、14、15、17、18、19、20、21、22、23、24），您可以使用長除法方法

3. 1 到 25 中哪些數字的平方根介於 2 和 3 之間？

1 到 25 的平方根數值介於 2 和 3 之間的是 $\mathrm{\sqrt{4}(2)\:,\:\sqrt{5}(2.236)\:,\:\sqrt{6}(2.449)\:,\:\sqrt{7}(2.646)\:,\:\sqrt{8}(2.828)\:,\:\sqrt{9}(3)}$

4. 25 的平方根的值是多少？

$\mathrm{\sqrt{25}\:的值是\:5}$

5. 1 到 25 的平方根範圍是有理數嗎？

數字 1、4、9、16 和 25 是完全平方數，因此它們的平方根是整數。因此，它們可以用 $\mathrm{\frac{p}{q}}$ 的形式表示，其中 p 和 q 是互質整數，且 $\mathrm{q\neq\:0}$。