資料結構
網路
RDBMS
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究關於一點繞另一點旋轉180度後的反射
你如何理解標題“關於一點繞另一點旋轉180度後的反射”？讓我們在這篇文章中解讀它。
假設我們在二維平面上有兩個點 (x1, y1) 和 (x2, y2)。
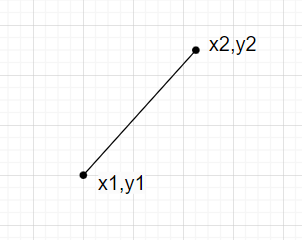
其中 (x2, y2) 是旋轉點，(x1, y1) 是要反射的點。
現在，假設 x1,y1 繞 x2,y2 旋轉 180 度，我們得到 x1`,y1`。
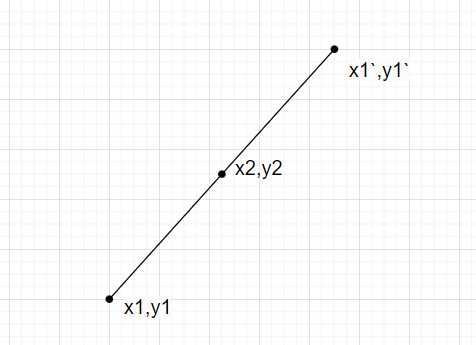
現在，我們可以觀察到，如果我們在二維平面上給出兩個點，其中一個點繞另一個點旋轉，則會得到三個共線點，並且旋轉點的另一個點也位於連線這三個點的直線的中間。
基於這些觀察結果，我們可以使用以下步驟來找到反射點的座標。
計算要反射的點和旋轉點之間的差值。也就是說，計算 (x1−x2) 和 (y1−y2)。
要反射該點，我們需要將該差值新增到旋轉點。也就是說，反射點將是 (x2+(x2−x1), y2+(y2−y1))。
簡化方程，我們得到反射點為 (2x2−x1, 2y2−y1)。
因此，要反射一點 (x1, y1) 繞另一點 (x2, y2) 旋轉 180 度，我們需要使用方程 (2x2−x1, 2y2−y1) 計算反射點。
例如，假設我們有一個點 (4, 6)，需要繞另一個點 (2, 2) 旋轉 180 度進行反射。反射點可以計算為 (2*2−4, 2*2−6)，即 (0, −2) 或簡化後的 (0, 2)。
方法
現在，我們對解決這個問題的邏輯有了清晰的認識。讓我們記下將討論的邏輯轉換為程式的分步方法。
將兩個點的座標作為使用者輸入。
使用公式 (x2+(x2−x1), y2+(y2−y1)) 計算反射點的座標。
將反射點列印到控制檯。
C++ 程式碼實現
紙上得來終覺淺，絕知此事要躬行。現在讓我們來寫一些程式碼。
這是查詢一點繞另一點旋轉180度後的反射座標的 C++ 實現。
示例
#include <iostream>
#include <cmath>
using namespace std;
int main() {
double x1 = 0;
double y1 = 0;
double x2 = 1;
double y2 = 1;
// Calculate the coordinates of the reflected point
double xr = x2 + (x2 - x1);
double yr = y2 + (y2 - y1);
cout << "The reflection of point (" << x1 << ", " << y1 << ") at 180-degree rotation of point (" << x2 << ", " << y2 << ") is (" << xr << ", " << yr << ").";
return 0;
}
輸出
The reflection of point (0, 0) at 180-degree rotation of point (1, 1) is (2, 2).
空間複雜度：O(1)
時間複雜度：O(1)
結論
在這篇文章中，我們介紹了計算反射點座標的邏輯，即一點繞另一點旋轉180度後的反射，給定兩個點。希望您對所涉及的概念和執行的程式碼有清晰的瞭解。
172 次瀏覽
