資料結構
網路
RDBMS
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究實用變壓器空載執行
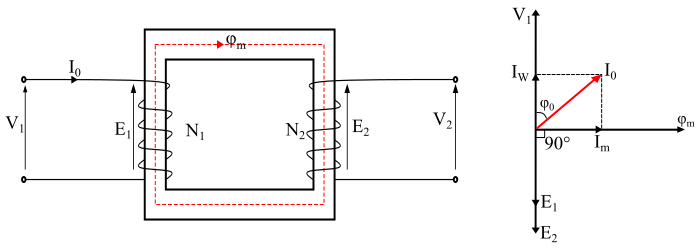
當實用變壓器的次級繞組開路時，則稱變壓器處於空載狀態（見圖）。在這種情況下，初級繞組將從電源汲取一個小的空載電流 I0，該電流提供鐵損和初級繞組中極少量的銅損。因此，初級空載電流 (I0) 與所加電壓 V1 的相位差不是 90°，而是滯後於它一個 φ0 角，該角小於 90°。
因此，
$$\mathrm{空載輸入功率，𝑃_{0} = 𝑉_{1}𝐼_{0} cos\varphi_{0}}$$
從相量圖可以看出，空載初級電流 (I0) 可以分解成兩個互相垂直的分量，即有功分量和磁化分量。
有功分量
分量 IW 與所加電壓 V1 同相，稱為有功分量或鐵損分量。空載電流的這一分量負責提供鐵損和變壓器中極少量的初級繞組銅損。IW 由下式給出：
$$\mathrm{𝐼_{𝑊} = 𝐼_{0} cos\varphi_{0}}$$
磁化分量
分量 Im 滯後於所加電壓 V1 90°，稱為空載電流的磁化分量。磁化分量負責產生變壓器鐵芯中的互感磁通 φm，並由下式給出：
$$\mathrm{𝐼_{𝑚} = 𝐼_{0} sin \varphi_{0}}$$
因此，空載電流 I0 是 IW 和 Im 的相量和，即
$$\mathrm{𝐼_{0} = \sqrt{𝐼_{𝑊}^{2} + 𝐼_{𝑚}^{2}}}$$
此外，空載功率因數由下式給出：
$$\mathrm{cos \varphi_{0} =\frac{𝐼_{𝑊}}{𝐼_{0}}}$$
需要注意的是，在實用變壓器中，空載時的初級繞組銅損非常小，可以忽略不計。因此，實用變壓器的空載輸入功率等於變壓器鐵芯中的鐵損，即
$$\mathrm{空載輸入功率， 𝑃_{0} = 鐵損}$$
此外，在空載時，次級繞組中沒有電流流動。因此，E2 = V2。
實用變壓器的空載等效電路
當變壓器處於空載狀態時，次級繞組中沒有電流流動。儘管初級繞組汲取了一個小的空載電流 (I0)，該電流提供磁化電流 (Im) 以在鐵芯中產生磁通，以及電流 IW 以提供鐵芯損耗。因此，空載初級電流被分成兩個分量，因此可以用兩個並聯支路表示，這兩個並聯支路由一個與初級繞組並聯的並聯電路 R0 – Xm 組成。
電阻 R0 稱為鐵損電阻，表示鐵損（即磁滯損耗和渦流損耗），因此電流 IW 流過 R0 支路。電感抗 Xm 稱為磁化電抗，表示一個無損線圈，用於在鐵芯中產生磁通，因此磁化電流 Im 流過它。
鐵損電阻 (R0) 由下式給出：
$$\mathrm{𝑅_{0} =\frac{𝑉_{1}}{𝐼_{𝑊}}}$$
磁化電抗 (Xm) 由下式給出：
$$\mathrm{𝑋_{𝑚} =\frac{𝑉_{1}}{𝐼_{𝑚}}}$$
需要注意的是，在實用變壓器中，電流 IW 與電流 Im 相比非常小。因此，實用變壓器的空載功率因數 (cosφ0) 非常小。
數值例子
一個 240/2200 V 變壓器汲取 5 A 的空載電流並吸收 200 W。如果初級繞組的電阻為 0.08 Ω。確定以下內容 -
鐵損
空載功率因數
空載電流的有功分量
磁化電流
解決方案
變壓器在空載時吸收的功率提供鐵損和初級繞組銅損。因此，
$$\mathrm{初級繞組銅損 = 𝐼_{0}^{2}𝑅_{1} = 5^2 × 0.08 = 2\:W}$$
鐵損
$$\mathrm{鐵損 = 𝑃_{0} − 初級繞組銅損}$$
$$\mathrm{⇒ 鐵損 = 200 − 2 = 198 \:W}$$
空載功率因數
$$\mathrm{cos \varphi_{0} =\frac{𝑃_{0}}{𝑉_{1}𝐼_{0}}=\frac{200}{240 × 5}= 0.167 (滯後)}$$
空載電流的有功分量
$$\mathrm{𝐼_{𝑊} = 𝐼_{0} cos\varphi_{0} = 5 × 0.167 = 0.835 A}$$
磁化電流
$$\mathrm{I_{m}=\sqrt{I_0^2-I_W^2}=\sqrt{(5)^{2}-(0.835)^{2}}=4.93\:A}$$
6K+ 次瀏覽
