資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究負載下的實際變壓器
當負載阻抗連線到實際變壓器的次級繞組時，則稱變壓器處於負載狀態，並汲取流經次級繞組和負載的負載電流。
我們將考慮以下兩種情況來分析實際變壓器：
情況 1 - 當假設變壓器沒有繞組電阻和漏磁通時
該圖顯示了一個實際變壓器，假設忽略了繞組電阻和漏抗。根據此假設，
$$\mathrm{𝑉_{1} = 𝐸_{1}\: 和 \:V_{2} = 𝐸_{2}}$$
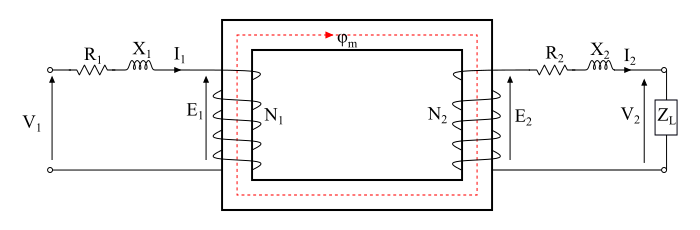
考慮一個感性負載連線到次級繞組，導致次級電流 I2 落後於次級電壓 V2 一個角度 ϕ2。在這種情況下，總初級電流 I1 必須滿足兩個要求：
- 首先，它必須提供空載電流 I0 以產生鐵損和變壓器鐵芯中的磁通量。
- 其次，它必須提供電流 I’2 以抵消次級電流 I2 的退磁作用。
電流 I’2 的大小由下式給出：
$$\mathrm{𝑁_{1}I'_{2}= 𝑁_{2}I_{2}}$$
$$\mathrm{⇒ I'_{2}=\frac{𝑁_{2}}{𝑁_{1}}I_{2} = 𝐾I_{2}}$$
因此，負載條件下實際變壓器汲取的總初級電流由 I’2 和 I0 的相量和給出，即
$$\mathrm{𝑰_{𝟏} = 𝑰'_{𝟐}+ 𝑰_{𝟎}}$$
其中，
$$\mathrm{𝐼’_{2} = − 𝐾I_{2}}$$
負號表示電流 I’2 與電流 I2 相差 180°。
相量圖顯示，兩個電動勢 E1 和 E2 都落後於互磁通 (ϕm) 90°。電流 I’2 表示初級電流的一部分，該部分抵消了次級電流 (I2) 的退磁作用。因此，電流 I’2 必須與 I2 反相。相量 I0 表示變壓器的空載電流。I’2 和 I0 的相量和表示總初級電流 (I1)。因此，
$$\mathrm{初級功率因數 = cos \varphi_{1}}$$
$$\mathrm{次級功率因數 = cos \varphi_{2}}$$
因此，
$$\mathrm{輸入功率，𝑃_{1} = 𝑉_{1}𝐼_{1} cos \varphi_{1}}$$
$$\mathrm{輸出功率，𝑃_{2} = V_{2}I_{2} cos \varphi_{2}}$$
情況 2 - 當變壓器具有繞組電阻和漏磁通時
該圖顯示了一個具有繞組電阻和漏抗的實際變壓器。這是實際變壓器中存在的實際情況。這裡，部分施加電壓會降落在初級繞組電阻 R1 和漏抗 X1 上，因此初級電動勢 (E 1) 將小於施加電壓 V1。
類似地，在次級繞組電阻 R2 和漏抗 X2 上存在電壓降，因此次級繞組端子上的電壓 V2 將小於次級電動勢 (E2)。
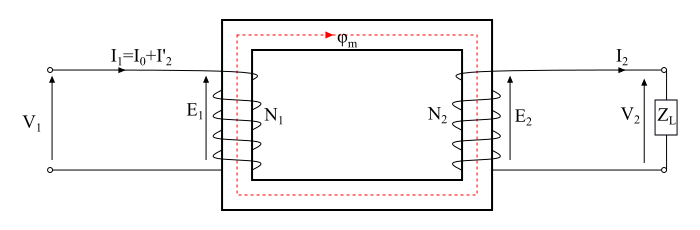
現在，考慮一個感性負載連線到變壓器的次級繞組，導致次級電流 I2 落後於次級電壓 V2 一個角度 ϕ2，並且總初級電流 (I1) 必須滿足兩個要求：
- 首先，它必須提供空載電流 I0 以產生鐵損和變壓器鐵芯中的磁通量。
- 其次，它必須提供電流 I’2 以抵消次級電流 I2 的退磁作用。
電流 I'2 的大小由下式給出：
$$\mathrm{𝑁_{1}I'_{2}= 𝑁_{2}I_{2}}$$
$$\mathrm{⇒ I'_{2} =\frac{𝑁_{2}}{𝑁_{1}}I_{2} = 𝐾I_{2}}$$
因此，負載條件下實際變壓器汲取的總初級電流由 I’2 和 I0 的相量和給出，即
$$\mathrm{𝑰_{𝟏} = 𝑰'_{𝟐} + Ｉ_{𝟎}}$$
其中，
$$\mathrm{𝐼’_{2} = − 𝐾I_{2}}$$
負號表示電流 I’2 與電流 I2 相差 180°。
現在，透過在初級迴路和次級迴路中應用 KVL，我們可以得到施加的初級電壓 (V1) 和次級端電壓 (V2) 為：
$$\mathrm{𝑽_{𝟏} = −𝑬_{𝟏} + 𝑰_{𝟏}(𝑹_{𝟏} + 𝒋𝑿_{𝟏})}$$
$$\mathrm{⇒ 𝑽_{𝟏} = −𝑬_{𝟏} + 𝑰_𝟏𝒁_𝟏}$$
和，
$$\mathrm{𝑽_{𝟐} = 𝑬_{𝟐} − 𝑰_{𝟐}(𝑹_{𝟐} + 𝒋𝑿_{𝟐})}$$
$$\mathrm{⇒ 𝑽_{𝟐} = 𝑬_{𝟐} − 𝑰_𝟐𝒁_𝟐}$$
粗體字母表示相量和。
從相量圖可以看出，兩個電動勢 E1 和 E2 都落後於互磁通 (ϕm) 90°。電流 I’2 表示初級電流，以抵消次級電流 (I2) 的退磁作用，該電流與 I2 反相。電流 I0 是變壓器的空載電流。因此，總初級電流 (I1) 由 I’2 和 I0 的相量和獲得。
此外，初級電壓 (V1) 透過將 I1R1 和 I1X1 的降落（相量和）加到反電動勢 (– E1) 上而獲得。次級端電壓 V2 透過從電動勢 (E2) 中減去 (相量差) I2R2 和 I2X2 而獲得。
輸入和輸出功率因數由下式給出：
$$\mathrm{輸入功率因數 = cos\varphi_1}$$
$$\mathrm{輸出功率因數 = cos\varphi_2}$$
此外，變壓器的輸入和輸出功率由下式給出：
$$\mathrm{輸入功率，𝑃1 = 𝑉_{1}𝐼_{1} cos \varphi_1}$$
$$\mathrm{輸出功率，𝑃2 = V_{2}I_{2} cos \varphi_2}$$
數值示例
一個 440/120 V 單相變壓器汲取 6 A 的空載電流，功率因數為 0.3 滯後。如果次級繞組以 0.85 滯後功率因數提供 100 A 的電流。確定初級繞組汲取的電流。
解決方案
這裡，初級電流 I1 由 I’2 和 I0 的相量和給出，因此，
$$\mathrm{cos\varphi_0 = 0.3;\:\: \therefore\:\: \varphi_0 = 72.54°}$$
$$\mathrm{cos\varphi_2 = 0.85;\:\: \therefore \:\:\varphi_2 = 31.79°}$$
現在，變壓比為：
$$\mathrm{𝐾 =\frac{V_{2}}{𝑉_{1}}=\frac{120}{440} =\frac{3}{11}}$$
因此，
$$\mathrm{I'_{2}= 𝐾I_{2} = (\frac{3}{11}) × 100 = 27.27 A}$$
參考相量圖，I’2 和 I0 之間的角度為
$$\mathrm{\theta = 72.54 − 31.79 = 40.75°}$$
現在，使用平行四邊形定則求向量和，初級電流為
$$\mathrm{I_{1} = \sqrt{(I'_{2})^2 + (𝐼_{0})^2 + 2I_{0}I'_{2}cos \theta}}$$
$$\mathrm{⇒ 𝐼_{1} = \sqrt{(27.27)^2 + (6)^2 + (2 × 6 × 27.27 × cos 40.75)} = 32.05 A}$$
7K+ 次檢視
