資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究同步發電機中的節距因數或線圈跨距因數
線圈跨距或線圈節距定義為線圈兩側之間的距離。
極距定義為一個磁極中心線到下一個磁極中心線的角度距離。無論機器上有多少個磁極，極距始終為 180° 電氣角。
當線圈跨距為 180° 電氣角時，稱為全節距線圈。
當線圈跨距小於 180° 電氣角時，稱為短節距線圈或分段節距線圈。
分段節距線圈也稱為絃線圈。使用分段節距線圈的定子繞組稱為弦繞組。
如果線圈跨距減少了 α 電氣角，則線圈跨距將為 (180 − α) 電氣度。
對於全節距線圈，兩個線圈邊跨越的距離正好等於 180° 電氣角的極距。因此，全節距線圈中產生的電壓使得線圈邊電壓同相。
設 $𝐸_{𝐶1}$ 和 $𝐸_{𝐶2}$ 是線圈兩邊產生的電壓，$𝐸_{𝐶}$ 是線圈的合成電壓。然後，
$$\mathrm{𝑬_{𝑪} = 𝑬_{𝑪𝟏} + 𝑬_{𝑪𝟐}}$$
由於 $𝐸_{𝐶1}$ 和 $𝐸_{𝐶2}$ 同相，因此合成線圈電壓等於它們的算術和（參考全節距線圈圖）。
$$\mathrm{∴\:𝐸_{𝐶} = 𝐸_{𝐶1} + 𝐸_{𝐶2}}$$
如果單個線圈的線圈跨距小於 180° 電氣角的極距，即短節距線圈的情況，則每個線圈邊產生的電壓不同相。合成線圈電壓 $𝐸_{𝐶}$ 等於 $𝐸_{𝐶1}$ 和 $𝐸_{𝐶2}$ 的相量和。
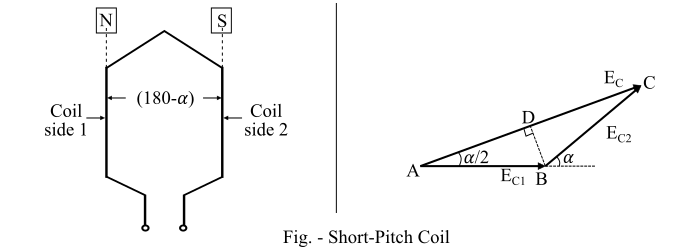
如果線圈跨距減少了 α 電氣角，則線圈跨距為 (180 − α) 電氣度。兩個線圈邊產生的電壓 $𝐸_{𝐶1}$ 和 $𝐸_{𝐶2}$ 相互之間將相差 α° 電氣角。$𝐸_{𝐶1}$ 和 $𝐸_{𝐶2}$ 的相量和為 $𝐸_{𝐶}$ = 𝐴𝐶（參考短節距線圈圖）。
線圈跨距因數或節距因數定義為短節距線圈中產生的電壓與全節距線圈中產生的電壓之比。線圈跨距因數也稱為弦距因數。
$$\mathrm{線圈跨距因數, 𝑘_{𝐶} =\frac{短節距線圈產生的電壓}{全節距線圈產生的電壓}}$$
參考相量圖，
$$\mathrm{𝑘_{𝐶} =\frac{兩個線圈邊電壓的相量和}{兩個線圈邊電壓的算術和}=\frac{𝐴𝐶}{2𝐴𝐵}}$$
$$\mathrm{\Rightarrow\:𝑘_{𝐶} =\frac{2𝐴𝐷}{2𝐴𝐵}= cos\left(\frac{α}{2}\right)}$$
對於全節距線圈，
$$\mathrm{α = 0°;\:\:\:cos\frac{α}{2}= 1;\:\:\:or\:\:\: 𝑘_{𝐶} = 1}$$
對於短節距線圈，
$$\mathrm{𝑘_{𝐶} < 1}$$
弦繞法的優點
弦繞法的優點如下：
由於弦繞縮短了繞組的端部，因此可以節省導體材料。
弦繞或短節距可以減少失真諧波的影響，從而改善產生的電壓波形，使其更接近正弦波。
12K+ 次檢視
