物理 - 球面透鏡

介紹

• 由兩個表面（其中一個或兩個表面是球形的）包圍的透明材料（通常是玻璃）稱為“球面透鏡”。

凸透鏡

• 一個透鏡可能有兩個向外凸起的球面（如下圖所示），稱為凸透鏡或雙凸透鏡。

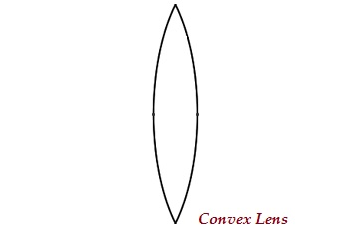
• 此透鏡的中間部分凸起（較厚），兩端較窄。

• 凸透鏡會匯聚光線；因此，它也稱為**會聚透鏡**。

凹透鏡

• 一個透鏡可能有兩個向內彎曲的球面（如下圖所示），稱為凹透鏡或雙凹透鏡。

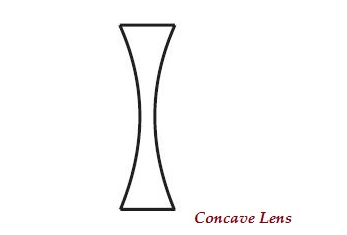
• 此透鏡的中間部分較窄（向內彎曲），兩端較厚。

• 凹透鏡會發散光線；因此，它也稱為**發散透鏡**。

• 一個透鏡，無論是凹透鏡還是凸透鏡，都有兩個球面，每個球面都構成球的一部分。這些球的中心稱為**曲率中心**，用英文字母“**C**”表示。

• 由於有兩個曲率中心，因此分別表示為“C₁”和“C₂”。

• 穿過透鏡兩個曲率中心的假想直線稱為**主軸**。

• 光心是透鏡的中心點。它用“**O**”表示。

• 光圈是球面透鏡圓形輪廓的實際直徑。

• 透鏡的主焦點用“**F**”表示。

• 一個透鏡通常有兩個焦點，分別表示為F₁和F₂。

• **焦距**是透鏡的主焦點和光心之間的距離。它用“**f**”表示。

• 下表說明了凸透鏡成像的性質和位置：

物體的位 置	像的位置	像的大小	像的性質	成像
無限遠	在焦點F2處	高度縮小，點狀	實像，倒立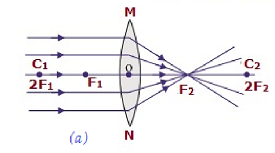
超過2F1	在F2和2F2之間	縮小	實像，倒立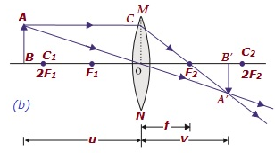
在2F1處	在2F2處	相同大小	實像，倒立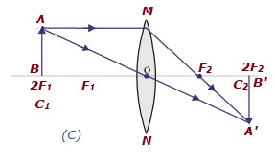
在F1和2F1之間	超過2F2	放大	實像，倒立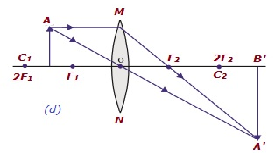
在焦點F1處	無限遠	無限大或高度放大	實像，倒立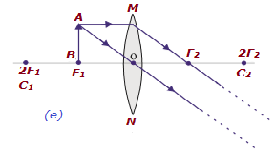
在焦點F1和光心O之間	與物體位於透鏡的同一側	放大	虛像，正立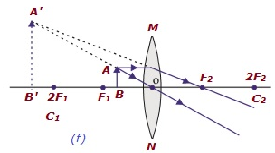

• 下表說明了凹透鏡成像的性質和位置：

物體的位 置	像的位置	像的相對大小	像的性質	成像
無限遠	在焦點F1處	高度縮小，點狀	虛像，正立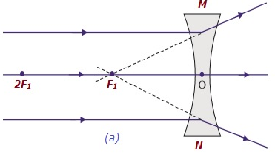
在無限遠和透鏡的光心O之間	在F1和光心O之間	縮小	虛像，正立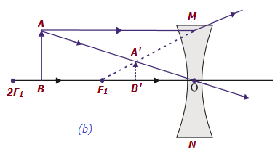

透鏡公式

• 公式表示為：

$$ \frac{1}{v} - \frac{1}{u} = \frac{1}{f} $$

• 透鏡公式表示物體距離（即**u**）、像距（即**v**）和透鏡焦距（即f）之間的關係。