物理 - 萬有引力

引言

• 宇宙中所有天體都相互吸引，這些天體之間的吸引力稱為萬有引力。

萬有引力定律

• 宇宙中的每個物體都具有吸引其他每個物體的特性，這種力與它們的質量的乘積成正比，與它們之間距離的平方成反比（見下圖）。

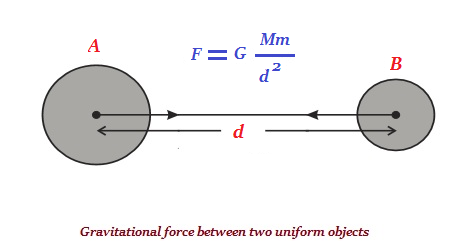
• F = 物體‘A’和‘B’之間的吸引力

• M = ‘A’的質量

• m = ‘B’的質量

• d² = ‘A’和‘B’之間距離的平方

• G = 比例常數，稱為萬有引力常數。

• G的SI單位為N m² kg^–2。它是透過代入力的單位、距離和質量（如下式所示）得到的：

$$G = \frac{Fd^2}{M \times m}$$

• 亨利·卡文迪許計算出‘G’的值為6.673 × 10^–11 N m² kg^–2。

• 亨利·卡文迪許使用靈敏的天平找到了‘G’的值。

萬有引力定律的意義

• 以下是萬有引力定律的重要意義：

  • 它解釋了將所有物體（包括人類）束縛在地球上的力

  • 它描述了月球繞地球執行的運動

  • 它解釋了行星繞太陽執行的運動

  • 它闡明瞭由月球和太陽引起的潮汐

自由落體

• 當物體落向地球時，會涉及加速度；這種加速度是由地球的萬有引力產生的。

• 由地球的萬有引力產生的加速度稱為地球的萬有引力加速度（或重力加速度）。

• 由萬有引力產生的加速度用g表示。

• 由於地球的半徑向赤道方向增加（從兩極），因此‘g’在兩極的值大於赤道。

g的值

• g的值計算如下：

$$g = G\frac{M}{R^2}$$

• G = 萬有引力常數，其值為6.7 × 10^–11 N m² kg^-2

• M = 地球的質量，其值為6 × 10²⁴ kg

• R = 地球的半徑，其值為6.4 × 10⁶ m

• 所以，

$$g = \frac{6.7 \: \times 10^{-11} \: Nm^2 \: kg^{-2} \: \times \: 6 \: \times 10^{24} \: kg}{(6.4 \: \times 10^6 \: m)^2}$$

$=9.8 \: m \: s^{-2}$

• 因此，地球的萬有引力加速度（g）值為9.8 m s^-2。