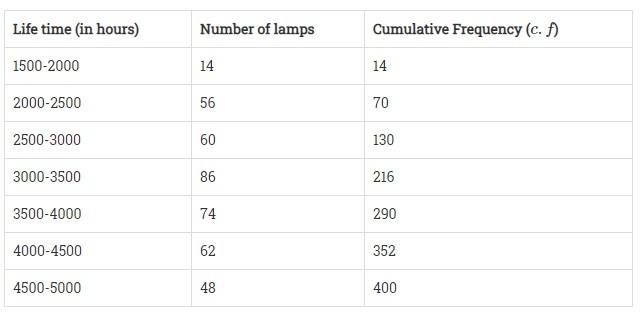
下表給出了 400 支霓虹燈的使用壽命分佈

壽命：（小時）	燈的數量
1500-2000	14
2000-2500	56
2500-3000	60
3000-3500	86
3500-4000	74
4000-4500	62
4500-5000	48

求中位壽命。

已知

給定的表格給出了 400 支霓虹燈的使用壽命分佈。

要求

我們需要求出中位壽命。

解答

這裡，

$N = 400$

$\frac{N}{2} = \frac{400}{2} = 200$

剛好大於 $\frac{N}{2}$ 的累積頻率是 216，對應的組是 3000 – 3500。

這意味著，3000– 3500 是中位陣列。

因此，

$l = 3000, f = 86, F = 130$ 以及 $h = (3500 - 3000) = 500$

中位數 $=\mathrm{l}+\frac{\frac{\mathrm{N}}{2}-\mathrm{F}}{\mathrm{f}} \times \mathrm{h}$

$=3000+\frac{200-130}{86} \times 500$

$=3000+\frac{70}{86} \times 500$

$=3000+\frac{35000}{86}$

$= 3000 + 406.98$

$= 3406.98$

中位壽命是 3406.98 小時。

教程點

更新於： 2022 年 10 月 10 日

35 次檢視

開啟你的 職業生涯

透過完成課程獲得認證

開始學習