資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
服裝設計
法學畫一條長度為\( 12.8 \mathrm{~cm} \)的線段。使用圓規將其分成四個相等的部分。透過實際測量進行驗證。
待辦事項
我們必須使用圓規將$12.8\ cm$長的線段分成四個相等的部分，並透過實際測量進行驗證。
解答
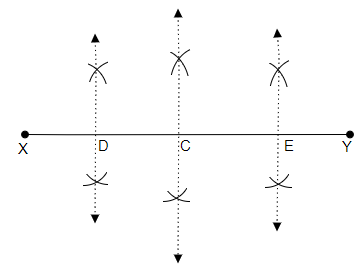
作圖步驟
(i) 我們畫一條長度為$12.8\ cm$的線段$\overline{XY}$。現在，用圓規取大於$\overline{XY}$長度一半的距離。
(ii) 現在，分別將圓規的針尖放在點X和點Y上。讓我們在$\overline{XY}$線段上方畫出兩條相交的弧。同樣地，分別將圓規的針尖放在點X和點Y上。讓我們在$\overline{XY}$線段下方畫出另外兩條相交的弧。
(iii) 然後，讓我們畫一條線段連線上下方弧線的交點，並將這條垂直平分線與$\overline{XY}$的交點命名為C。因此，C成為$\overline{XY}$的中點。
(iv) 以類似的方式，用圓規取大於$\overline{CB}$長度一半的距離。現在，分別將圓規的針尖放在點C和點B上。讓我們在$\overline{XY}$線段上方畫出兩條相交的弧。
(v) 同樣地，分別將圓規的針尖放在點C和點B上。讓我們在$\overline{XY}$線段下方畫出另外兩條相交的弧。然後，讓我們畫一條線段連線上下方弧線的交點，並將這條垂直平分線與$\overline{XY}$的交點命名為E。
(vi) 因此，E成為$\overline{CY}$的中點。以類似的方式，用圓規取大於$\overline{AX}$長度一半的距離。
(vii) 現在，分別將圓規的針尖放在點X和點C上。讓我們在$\overline{XC}$線段上方畫出兩條相交的弧。同樣地，分別將圓規的針尖放在點X和點C上。讓我們在$\overline{XY}$線段下方畫出另外兩條相交的弧。
(ix) 然後，讓我們畫一條線段連線上下方弧線的交點，並將這條垂直平分線與$\overline{XY}$的交點命名為D。因此，D成為$\overline{XC}$的中點。
60次瀏覽
