一個木塊以\( 10 \mathrm{~m} / \mathrm{s} \)的速度運動，並受到一個大小為$100N$的力，此外摩擦力也作用在木塊上。求木塊的加速度。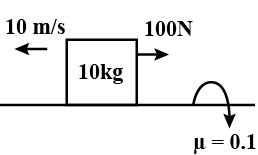"\n

已知

質量，$m$ = 10 kg

速度，$v$ = 10 m/s

力，$F$ = 100 N

求解：木塊的加速度，或木塊的負加速度$(a_r)$。

解答

我們知道摩擦力表示為-

$f=\mu N$

$f$ = 摩擦力

$\mu$ = 摩擦係數

$N$ = 垂直壓力

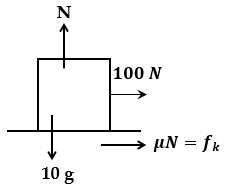
由於存在相對運動

因此動摩擦力將減小這種相對運動。

$f_k=\mu N$

$f_k=\mu mg$     $(\because N=mg)$

將給定值代入上式，得到-

$f_k=0.1\times {10}\times {10}=10N$

因此，木塊上的合力將為-

$100N+10N=110N$

現在，我們知道加速度，$a$ 表示為-

$a=\frac {F}{m}$

因此，這裡-

$a_r=\frac {F_{net}}{m}$

$a_r=\frac {110}{10}$

$a=11m/s^2$

因此，木塊的加速度，或木塊的負加速度$(a_r)$為11m/s².

Tutorialspoint

更新於: 2022年10月10日

46 次瀏覽

開啟你的職業生涯

透過完成課程獲得認證

立即開始