
NLP - 詞級別分析
本章我們將瞭解自然語言處理中的詞級別分析。
正則表示式
正則表示式 (RE) 是一種用於指定文字搜尋字串的語言。RE 幫助我們使用包含在模式中的特殊語法來匹配或查詢其他字串或字串集。正則表示式在 UNIX 和 MS WORD 中以相同的方式用於搜尋文字。許多搜尋引擎都使用許多 RE 功能。
正則表示式的屬性
以下是 RE 的一些重要屬性:
美國數學家斯蒂芬·科爾·克萊尼(Stephen Cole Kleene)將正則表示式語言形式化。
RE 是用特殊語言編寫的公式,可用於指定簡單的字串類,即符號序列。換句話說,我們可以說 RE 是表徵字串集的代數符號。
正則表示式需要兩樣東西,一個是我們要搜尋的模式,另一個是我們需要從中搜索的文字語料庫。
數學上,正則表示式可以定義如下:
ε 是一個正則表示式,表示該語言包含空字串。
φ 是一個正則表示式,表示它是空語言。
如果X 和Y 是正則表示式,則
X,Y
X.Y(XY 的串聯)
X+Y(X 和 Y 的並集)
X*,Y*(X 和 Y 的 Kleene 閉包)
也是正則表示式。
如果一個字串是從上述規則匯出的,那麼它也應該是一個正則表示式。
正則表示式的示例
下表顯示了一些正則表示式的示例:
| 正則表示式 | 正則集 |
|---|---|
| (0 + 10*) | {0, 1, 10, 100, 1000, 10000, … } |
| (0*10*) | {1, 01, 10, 010, 0010, …} |
| (0 + ε)(1 + ε) | {ε, 0, 1, 01} |
| (a+b)* | 它將是任意長度的 a 和 b 字串集,也包括空字串,即 {ε, a, b, aa, ab, bb, ba, aaa……}。 |
| (a+b)*abb | 它將是 a 和 b 字串集,以字串 abb 結尾,即 {abb, aabb, babb, aaabb, ababb, …………..}。 |
| (11)* | 它將是包含偶數個 1 的字串集,也包括空字串,即 {ε, 11, 1111, 111111, ………}。 |
| (aa)*(bb)*b | 它將是包含偶數個 a 後跟奇數個 b 的字串集,即 {b, aab, aabbb, aabbbbb, aaaab, aaaabbb, …………..}。 |
| (aa + ab + ba + bb)* | 它將是偶數長度的 a 和 b 字串,可以透過串聯 aa、ab、ba 和 bb 的任何組合(包括空字串)獲得,即 {aa, ab, ba, bb, aaab, aaba, …………..}。 |
正則集及其屬性
它可以定義為表示正則表示式值的集合,並具有特定屬性。
正則集的屬性
如果我們對兩個正則集進行並集運算,則結果集也應該是正則的。
如果我們對兩個正則集進行交集運算,則結果集也應該是正則的。
如果我們對正則集進行補集運算,則結果集也應該是正則的。
如果我們對兩個正則集進行差集運算,則結果集也應該是正則的。
如果我們對正則集進行反轉運算,則結果集也應該是正則的。
如果我們對正則集進行閉包運算,則結果集也應該是正則的。
如果我們對兩個正則集進行串聯運算,則結果集也應該是正則的。
有限狀態自動機
術語自動機源於希臘語“αὐτόματα”,意思是“自動的”,是自動機的複數形式,可以定義為一種抽象的自動推進計算裝置,它會自動遵循預定的操作序列。
具有有限數量狀態的自動機稱為有限自動機 (FA) 或有限狀態自動機 (FSA)。
數學上,自動機可以用一個 5 元組 (Q, Σ, δ, q0, F) 來表示,其中:
Q 是有限的狀態集。
Σ 是有限的符號集,稱為自動機的字母表。
δ 是轉移函式
q0 是處理任何輸入的初始狀態 (q0 ∈ Q)。
F 是 Q 的最終狀態集 (F ⊆ Q)。
有限自動機、正則文法和正則表示式之間的關係
以下幾點將使我們更清楚地瞭解有限自動機、正則文法和正則表示式之間的關係:
眾所周知,有限狀態自動機是計算工作的理論基礎,正則表示式是描述它們的一種方式。
我們可以說,任何正則表示式都可以實現為 FSA,任何 FSA 都可以用正則表示式來描述。
另一方面,正則表示式是一種表徵稱為正則語言的語言型別的方式。因此,我們可以說正則語言可以用 FSA 和正則表示式來描述。
正則文法(可以是右正則或左正則的形式文法)是表徵正則語言的另一種方式。
下圖顯示有限自動機、正則表示式和正則文法是描述正則語言的等效方式。
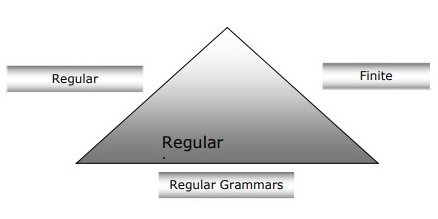
有限狀態自動機 (FSA) 的型別
有限狀態自動機分為兩種型別。讓我們看看這些型別是什麼。
確定性有限自動機 (DFA)
它可以定義為一種有限自動機,其中對於每個輸入符號,我們可以確定機器將移動到的狀態。它具有有限數量的狀態,這就是為什麼機器被稱為確定性有限自動機 (DFA) 的原因。
數學上,DFA 可以用一個 5 元組 (Q, Σ, δ, q0, F) 來表示,其中:
Q 是有限的狀態集。
Σ 是有限的符號集,稱為自動機的字母表。
δ 是轉移函式,其中 δ: Q × Σ → Q。
q0 是處理任何輸入的初始狀態 (q0 ∈ Q)。
F 是 Q 的最終狀態集 (F ⊆ Q)。
而在圖形上,DFA 可以用稱為狀態圖的有向圖來表示,其中:
狀態由頂點表示。
轉換由帶標籤的弧表示。
初始狀態由空的傳入弧表示。
最終狀態由雙圓圈表示。
DFA 示例
假設一個 DFA 為
Q = {a, b, c},
Σ = {0, 1},
q0 = {a},
F = {c},
轉移函式 δ 如表所示:
| 當前狀態 | 輸入 0 的下一狀態 | 輸入 1 的下一狀態 |
|---|---|---|
| A | a | B |
| B | b | A |
| C | c | C |
此 DFA 的圖形表示如下:
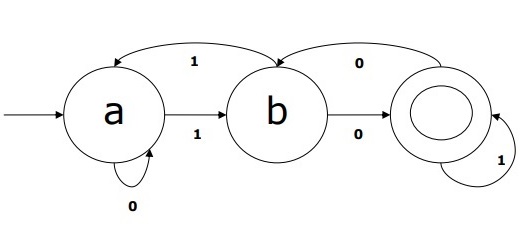
非確定性有限自動機 (NDFA)
它可以定義為一種有限自動機,其中對於每個輸入符號,我們無法確定機器將移動到的狀態,即機器可以移動到任何狀態組合。它具有有限數量的狀態,這就是為什麼機器被稱為非確定性有限自動機 (NDFA) 的原因。
數學上,NDFA 可以用一個 5 元組 (Q, Σ, δ, q0, F) 來表示,其中:
Q 是有限的狀態集。
Σ 是有限的符號集,稱為自動機的字母表。
δ:- 是轉移函式,其中 δ: Q × Σ → 2Q。
q0:- 是處理任何輸入的初始狀態 (q0 ∈ Q)。
F:- 是 Q 的最終狀態集 (F ⊆ Q)。
而在圖形上(與 DFA 相同),NDFA 可以用稱為狀態圖的有向圖來表示,其中:
狀態由頂點表示。
轉換由帶標籤的弧表示。
初始狀態由空的傳入弧表示。
最終狀態由雙圓圈表示。
NDFA 示例
假設一個 NDFA 為
Q = {a, b, c},
Σ = {0, 1},
q0 = {a},
F = {c},
轉移函式 δ 如表所示:
| 當前狀態 | 輸入 0 的下一狀態 | 輸入 1 的下一狀態 |
|---|---|---|
| A | a, b | B |
| B | C | a, c |
| C | b, c | C |
此 NDFA 的圖形表示如下:
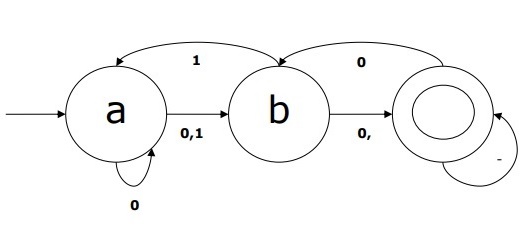
形態分析
術語形態分析與詞素的分析有關。我們可以將形態分析定義為識別單詞分解成稱為詞素的較小有意義單元的問題,從而為其產生某種語言結構。例如,我們可以將單詞 *foxes* 分解成兩個,*fox* 和 *-es*。我們可以看到,單詞 *foxes* 由兩個詞素組成,一個是 *fox*,另一個是 *-es*。
換句話說,我們可以說形態學是研究:
單詞的構成。
單詞的起源。
單詞的語法形式。
在單詞構成中使用字首和字尾。
語言的詞性是如何構成的。
詞素的型別
詞素是最小的意義單元,可以分為兩種型別:
詞幹
詞序
詞幹
它是單詞的核心有意義的單元。我們也可以說它是單詞的詞根。例如,在單詞 foxes 中,詞幹是 fox。
詞綴 - 顧名思義,它們為單詞添加了一些額外的含義和語法功能。例如,在單詞 foxes 中,詞綴是 -es。
此外,詞綴還可以細分為以下四種類型:
字首 - 顧名思義,字首位於詞幹之前。例如,在單詞 unbuckle 中,un 是字首。
字尾 - 顧名思義,字尾位於詞幹之後。例如,在單詞 cats 中,-s 是字尾。
中綴 - 顧名思義,中綴插入詞幹內部。例如,單詞 cupful 可以透過使用 -s 作為中綴變為複數 cupsful。
環繞詞綴 - 它們位於詞幹之前和之後。英語中環繞詞綴的例子很少。一個非常常見的例子是“A-ing”,其中我們可以使用 -A 位於詞幹之前,-ing 位於詞幹之後。
詞序
詞序將由形態分析決定。現在讓我們看看構建形態分析器的要求:
詞典
構建形態分析器的第一個要求是詞典,其中包括詞幹和詞綴的列表以及關於它們的 基本資訊。例如,諸如詞幹是名詞詞幹還是動詞詞幹等資訊。
形態句法
它基本上是詞素排序模型。換句話說,解釋哪些詞素類可以在單詞內部跟隨其他詞素類的模型。例如,形態句法事實是,英語複數詞素總是跟在名詞後面,而不是在名詞前面。
拼寫規則
這些拼寫規則用於模擬單詞中發生的更改。例如,將 y 轉換為 ie 的規則,例如 city+s = cities,而不是 citys。