不完全指定邏輯函式的最小化

---

在布林代數或邏輯代數中，邏輯函式是一個數學表示式，它指定邏輯電路的輸入和輸出之間的關係。布林函式可以分為兩種型別：**完全指定邏輯函式**和**不完全指定邏輯函式**。

完全指定邏輯函式是指其輸出對於每種可能的輸入組合都是確定或已定義的函式，而布林函式的輸出值至少對於一種輸入組合未指定的則稱為不完全指定邏輯函式。

在不完全指定邏輯函式中，未定義輸出的輸入變數組合稱為**無關項**。

在本文中，我們將透過示例討論不完全指定邏輯函式的最小化。

示例 1

將布林表示式最小化到其最小形式：

$$F\left ( A,B,C,D \right )=\sum m\left ( 0, 3, 7, 8, 9, 10, 11, 15 \right )+d\left ( 2,4 \right )$$

解答

我們可以觀察到，給定的布林函式有兩個無關項，即 2 和 4，因此它是不完全指定邏輯函式。我們可以使用卡諾圖 (Karnaugh Map) 最小化技術來最小化此函式。

給定不完全指定邏輯函式的卡諾圖表示如下面的圖 1 所示。

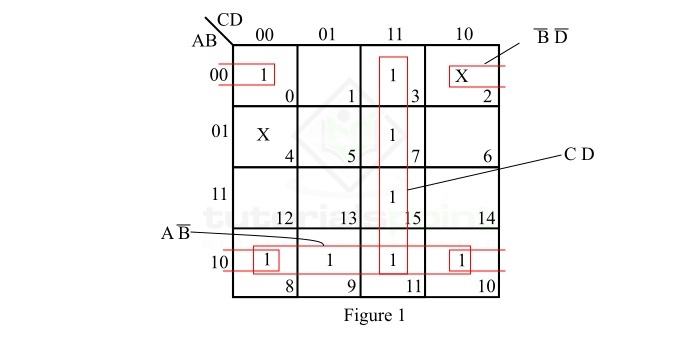
在圖 1 所示的卡諾圖中，簡化步驟如下：

• **步驟 1** - 沒有孤立的 1。

• **步驟 2** - 極小項 m₀ 與極小項 m₂（無關項）、m₈ 和 m₁₀ 構成一個四個方格。構成四個方格並將其讀取為 $\bar{B}\bar{D}$

• **步驟 3** - 極小項 m₃ 與極小項 m₇、m₁₁ 和 m₁₅ 構成一個四個方格。構成四個方格並將其讀取為 $CD$。

• **步驟 4** - 極小項 m₈ 與極小項 m₉、m₁₀ 和 m₁₁ 構成一個四個方格。構成四個方格並將其讀取為 $A\bar{B}$。

• **步驟 5** - 將所有乘積項寫成 SOP（積之和）形式。

因此，給定不完全指定邏輯函式的最小 SOP 表示式為：

$$F_{min}=\bar{B}\bar{D}+A\bar{B}+CD$$

示例 2

最小化以下布林表示式：

$$F\left ( A,B,C,D \right )=\sum m\left ( 1, 3, 7, 11, 15 \right )+d\left ( 0, 2, 5 \right )$$

解答

我們可以觀察到，給定的布林函式有三個無關極小項。因此，它是不完全指定邏輯函式。

現在，讓我們使用卡諾圖簡化技術將此表示式最小化到最小形式。給定函式的卡諾圖表示如圖 2 所示。

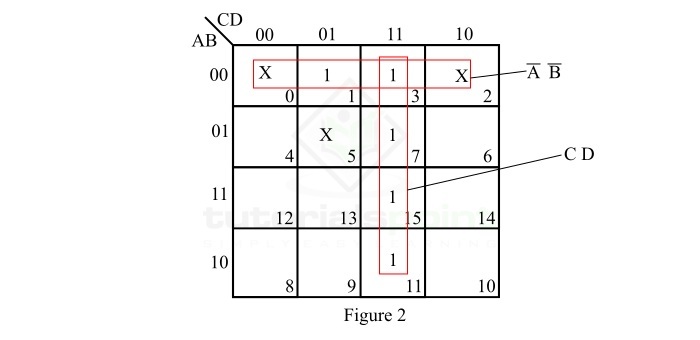
在圖 2 所示的卡諾圖中，不完全指定函式的最小化步驟如下：

• **步驟 1** - 沒有孤立的 1。

• **步驟 2** - 極小項 m1 與極小項 m₀（無關項）、m₂（無關項）和 m₃ 構成一個四個方格。構成四個方格並將其讀取為 $\bar{A}\bar{B}$。

• **步驟 3** - 極小項 m₇ 與極小項 m₇、m₁₁ 和 m₁₅ 構成一個四個方格。構成四個方格並將其讀取為 $CD$。

• **步驟 4** - 將所有乘積項寫成 SOP 形式。

因此，給定不完全指定邏輯函式的最小布爾表示式為：

$$F_{min}=\bar{A}\bar{B}+CD$$

這就是關於布林代數中不完全指定邏輯函式最小化的全部內容。