資料結構
網路
RDBMS
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究布林代數中的不完全指定函式
什麼是未完全指定的函式？
在布林代數中，如果一個布林函式或邏輯函式的輸出值只對其輸入子集已知，並且對於至少一個輸入組合，其輸出為“無關項”條件，則該函式稱為不完全指定函式。
因此，在不完全指定函式中，對於“無關項”組合，函式的值可以選擇為 0 或 1，具體取決於哪一個可以導致函式的更簡化的解。對於這些組合，卡諾圖 (K-Map) 中的條目標記為 X，表示該特定單元格可以取 0 或 1。
無關項組合
通常，我們擁有對輸入變數的每種組合都完全指定的布林表示式或函式。這意味著布林函式的每個最大項或最小項都指定為 0 或 1。但是，在某些情況下，對於某些輸入組合，由於輸入組合無效或輸出的精確值無關緊要，因此輸出值未指定。這些輸入變數的組合，其布林函式值未指定，稱為無關項組合。具有此類無關項組合的布林函式稱為不完全指定的布林函式。
現在，讓我們考慮以下示例，以便更深入地瞭解不完全指定的函式。
示例
考慮以下具有無關項條件的布林函式，
$$ F\left ( A,B,C \right )=\sum m\left ( 1,2,7 \right )+d\left ( 0,3,4 \right )$$
此布林函式的真值表如下所示：
| 輸入 | 輸出 | ||
|---|---|---|---|
| A | B | C | F |
| 0 | 0 | 0 | X |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | X |
| 1 | 0 | 0 | X |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
此函式可以在卡諾圖 (K-Map) 上表示，如下面的圖所示。
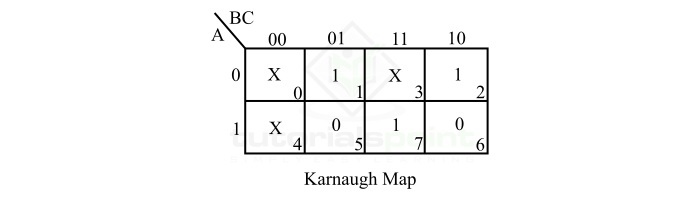
還有許多其他不完全指定的布林函式的示例。例如，在 Excess-3 程式碼系統中，二進位制組合 0000、0001、0010、1101、1110 和 1111 未指定，並且永遠不會出現在系統中。因此，這些稱為無關項組合。具有這些組合或其中任何一個組合的邏輯函式稱為不完全指定函式。
另一個示例是 8421 BCD 碼，其中二進位制組合 1010、1011、1100、1101、1110 和 1111 未指定，並且永遠不會出現在系統中。因此，對應於這些無效組合的布林函式的輸出是無關項。
結論
總之，如果布林表示式或邏輯函式中至少存在一個輸入變數組合，使得該組合的輸出未指定，並且該組合被視為無關項組合，則此類布林函式被稱為不完全指定的邏輯函式。
744 次檢視
