資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法學研究低通和高通濾波器波德圖
波德圖是線性系統的頻率響應圖，以對數圖的形式表示。在波德圖中，橫軸表示頻率（對數刻度），縱軸表示頻率響應函式的幅度或相位。
低通濾波器波德圖
RC低通濾波器的頻率響應函式或傳遞函式為：
$$\frac{V_{out}}{V_{in}}=\frac{A}{1+(j\omega\:T)}=\frac{A}{1+(j\omega\:/\omega_{0})}=\frac{A}{\sqrt{1+(\omega\:/\omega_{0})^{2}}}\angle\:-\tan^{-1}(\frac{\omega}{\omega_{0}})$$
其中：
T = 電路的時常數 = $1/\omega_{0}=RC$
A = 常數，並且
$\omega_{0}$ = 截止頻率
低通濾波器的波德幅度圖
幅度圖可以從傳遞函式的絕對值獲得，即：
$$|\frac{V_{out}}{V_{in}}|=20\log_{10}\frac{|A|}{|1+j\omega\:/\omega_{0}|}$$
當 $\omega\:<\omega_{0}$ 時，虛部遠小於實部，因此 $|1+j\omega\:/\omega_{0}|=1$，因此：
$$|\frac{V_{out}}{V_{in}}|_{dB}=20\log_{10}A-20\log_{10}\:1=20\log_{10}A$$
因此，在非常低的頻率下，頻率響應函式可以用斜率為零的直線來近似，這是波德圖的低頻漸近線。
當 $\omega\:>\omega_{0}$ 時，虛部遠大於實部，因此 $|1+j\omega\:/\omega_{0}|=|j\omega\:/\omega_{0}|$，因此：
$$|\frac{V_{out}}{V_{in}}|_{dB}=20\log_{10}A-20\log_{10}\:(\omega\:/\omega_{0})=20\log_{10}A-20\log_{10}\omega-20\log_{10}\omega_{0}$$
因此，在非常高的頻率下，頻率響應函式可以用斜率為(-20 dB/十倍頻程)的直線來近似，該直線與$\log\omega$在$\log\:\omega_{0}$處相交。這條線是波德圖的高頻漸近線。
當 $\omega=\omega_{0}$ 時，單極點的實部和虛部相等，所以 $|1+j\omega\:+\omega_{0}|=|1+j|=\sqrt{2}$，因此：
$$|\frac{V_{out}}{V_{in}}|_{dB}=20\log_{10}A-20\log_{10}\sqrt{2}=20\log_{10}A-3dB$$
因此，幅度圖可以用兩條在$\omega_{0}$處相交的直線來近似。
低通濾波器的波德相點陣圖
$$\angle(\frac{V_{out}}{V_{in}})=-\tan^{-1}(\frac{\omega}{\omega_{0}})$$
當 $\omega\rightarrow0$ 時，
$$\angle(\frac{V_{out}}{V_{in}})=-\tan^{-1}(\frac{\omega}{\omega_{0}})=0$$
當 $\omega=0$ 時，
$$\angle(\frac{V_{out}}{V_{in}})=-\tan^{-1}(\frac{\omega}{\omega_{0}})=-\frac{\pi}{4}$$
當 $\omega\rightarrow\infty$ 時，
$$\angle(\frac{V_{out}}{V_{in}})=-\tan^{-1}(\frac{\omega}{\omega_{0}})=-\frac{\pi}{2}$$
高通濾波器波德圖
高通濾波器的頻率響應或波德圖與低通濾波器的波德圖正好相反。
利用濾波器電路的傳遞函式或頻率響應函式，我們可以繪製頻率響應。
高通濾波器的波德幅度圖
$$\frac{V_{out}}{V_{in}}(j\omega)|=\frac{\omega}{\sqrt{\omega^{2}+(\omega_{0})^{2}}}=\frac{\omega}{\sqrt{\omega^{2}+(1/RC)^{2}}}$$
當 $\omega<\omega_{0}$ 時，幅度曲線以+20 dB/十倍頻程的斜率衰減低頻。因此，從初始點到截止頻率的區域稱為阻帶。
當 $\omega>\omega_{0}$ 時，濾波器電路將允許訊號透過，截止頻率點以上的區域稱為通帶。
當 $\omega=\omega_{0}$ 時，此時輸出電壓的幅度為輸入電壓的70.7%。
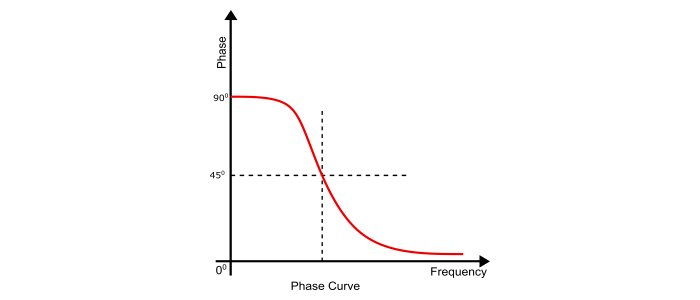
高通濾波器的波德相點陣圖
相點陣圖可以透過傳遞函式的相位方程獲得。
$$\angle(\frac{V_{out}}{V_{in}})=90^{\circ}-\tan^{-1}(\frac{\omega}{\omega_{0}})=90^{\circ}-\tan^{-1}(\omega\:RC)$$
當 $\omega\rightarrow0$ 時，
$$\angle(\frac{V_{out}}{V_{in}})=90^{\circ}-\tan^{-1}(\frac{\omega}{\omega_{0}})=\frac{\Pi}{2}$$
當 $\omega=0$ 時，
$$\angle(\frac{V_{out}}{V_{in}})=90^{\circ}-\tan^{-1}(\frac{\omega}{\omega_{0}})=\frac{\Pi}{4}$$
當 $\omega\rightarrow\infty$ 時，
$$\angle(\frac{V_{out}}{V_{in}})=90^{\circ}-\tan^{-1}(\frac{\omega}{\omega_{0}})=0$$
13K+ 次瀏覽
