資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝學
法學Python 實現數字帶通巴特沃斯濾波器
帶通濾波器是一種只允許特定頻率範圍內的訊號透過，而阻擋其他頻率範圍外訊號的濾波器。巴特沃斯帶通濾波器的設計目標是使其在通帶內的頻率響應儘可能平坦。以下是數字帶通巴特沃斯濾波器的規格說明。
濾波器的取樣率約為 40 kHz。
通帶截止頻率範圍為 1400 Hz 到 2100 Hz。
阻帶截止頻率範圍為 1050 Hz 到 2450 Hz。
通帶紋波為 0.4 分貝。
阻帶最小衰減為 50 分貝。
實現數字帶通巴特沃斯濾波器
實現數字帶通巴特沃斯濾波器是一個循序漸進的過程。讓我們詳細瞭解每個步驟。
步驟 1 − 首先，我們需要定義輸入訊號的取樣頻率 fs、下限截止頻率 f1、上限截止頻率 f2 和濾波器的階數。如果我們確定了較高的濾波器階數，則會導致更陡峭的滾降，從而造成相位失真。
步驟 2 − 接下來，我們需要使用下面的公式計算下限和上限截止頻率 f1 和 f2 的歸一化頻率 wn1 和 wn2。
$\mathrm{wn = 2 * fn / fs}$
步驟 3 − 之後，我們可以使用 scipy.signal.butter() 函式設計指定階數和歸一化頻率的巴特沃斯濾波器，並將 btype 引數指定為 band。
步驟 4 − 現在，我們將使用 scipy.signal.filtfilt() 函式對給定的輸入訊號應用濾波器，以執行零相位濾波。
示例
在下面的示例中，我們使用上述步驟實現數字帶通巴特沃斯濾波器。
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import butter, filtfilt
def butter_bandpass(lowcut, highcut, fs, order=5):
nyq = 0.5 * fs
low = lowcut / nyq
high = highcut / nyq
b, a = butter(order, [low, high], btype='band')
return b, a
def butter_bandpass_filter(data, lowcut, highcut, fs, order=5):
b, a = butter_bandpass(lowcut, highcut, fs, order=order)
y = filtfilt(b, a, data)
return y
fs = 1000
t = np.arange(0, 1, 1/fs)
f1 = 10
f2 = 50
sig = np.sin(2*np.pi*f1*t) + np.sin(2*np.pi*f2*t)
order = 4
filtered = butter_bandpass_filter(sig, f1, f2, fs, order)
print("The length of frequencies:",len(filtered))
print("The Butterworth bandpass filter output of first 50 frequencies:",filtered[:50])
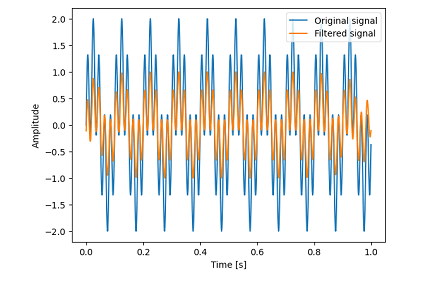
fig, ax = plt.subplots()
ax.plot(t, sig, label='Original signal')
ax.plot(t, filtered, label='Filtered signal')
ax.set_xlabel('Time [s]')
ax.set_ylabel('Amplitude')
ax.legend()
plt.show()
輸出
The length of frequencies: 1000 The Butterworth bandpass filter output of first 50 frequencies: [-0.11133763 0.06408296 0.22202113 0.34937958 0.4360314 0.47578308 0.46696733 0.41260559 0.32012087 0.20062592 0.06785282 -0.0631744 -0.17759655 -0.26216511 -0.30653645 -0.30428837 -0.2535591 -0.15724548 -0.02273955 0.13877185 0.31337781 0.48578084 0.64077163 0.76469778 0.84678346 0.88017133 0.86258464 0.79654483 0.68912261 0.55124662 0.39663647 0.24046415 0.09787411 -0.01749368 -0.0948334 -0.12722603 -0.11231195 -0.05251783 0.04518472 0.16996505 0.30819725 0.44479774 0.5647061 0.65436437 0.70305015 0.70393321 0.65475213 0.5580448 0.42091007 0.25432388]
更新於: 2023-10-31
瀏覽量 1K+
廣告