峰度 – 定義、示例、型別

峰度是一個統計術語，用於量化類似於偏度的分佈。與僅區分一個尾部中的絕對值與另一個尾部中的絕對值的偏度不同，峰度評估兩個尾部的極值。在具有強峰度的分佈中，尾部資料超過正態分佈的尾部。低峰度的範圍的尾部通常不如正態迴圈的尾部嚴重。

高峰度是投資者密切關注的一種趨勢，因為它可能導致利潤或損失的兩個方向都會出現更尖銳的結果。這與正常偏差或常規變化相比。峰度風險是賦予此指標的名稱，該指標向投資者發出了有關其資產的訊號。

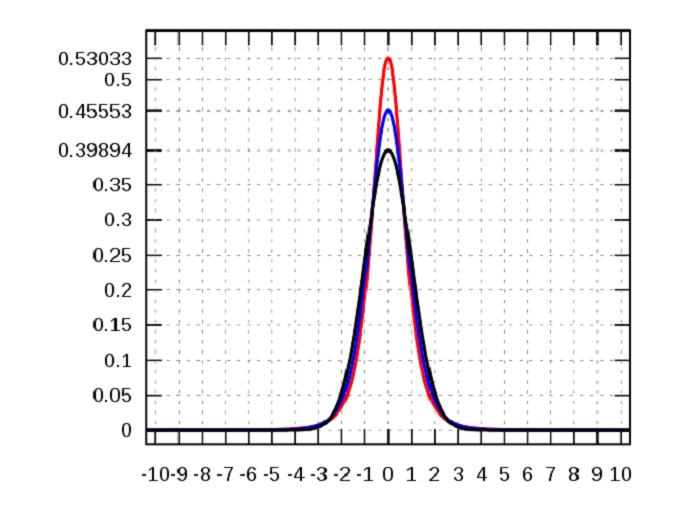
什麼是峰度？

峰度衡量分配尾部相對於分佈中心的總權重。當使用直方圖繪製正態資料時，可以觀察到一個鐘形峰值，其中大部分資料位於均值的 +/- 變化範圍內三個標準偏差內。在強峰度期間，此鐘形直方圖傾向於超出正常變化的長度。

在此統計工具中，有時在分佈峰值發生時會出現混淆。必須記住，峰度是形狀圖，與完整形狀相比，它提供了關於分佈尾部的整體情況。

在低峰度的情況下，分佈也可以非常尖銳，而在無限峰度的情況下，它可以完全正常或平坦，沒有任何偏差。因此，此工具計算並更多地關注“尾端性”，而不是峰值。

峰度的不同型別有哪些？

給定分佈的超額峰度決定了峰度的形式。超額峰度可以是正的或負的，也可以接近於零。

• 正態分佈 - 超額峰度

這種型別的模式通常以其超額峰度為零或接近零而被識別，這在遵循正態分佈的資料中可見。如果資料遵循正態分佈，則表明資料具有正態分佈。

• 尖頂分佈 – 正超額峰度

尖頂分佈表示正偏峰度。它的特徵是在兩側都有巨大的尾部，並且存在大量異常值。對於投資者而言，這可能意味著結果將是正或負的極端。因此，此圖表可能表明投資者在分佈的兩側進行投資的風險模式。

• 扁平分佈 – 負超額峰度

扁平分佈中的超額峰度為負，其特徵是扁平尾部分佈。扁平尾部表示分佈中的較小異常值。在金融環境中，投資回報的扁平分佈對投資者有利，因為這意味著更高的投資回報。

M S Faisal

更新於: 2021年8月11日

2K+ 次檢視

開啟您的 職業生涯

透過完成課程獲得認證

開始