基於教學學習最佳化的實現

---

簡介

基於教學學習最佳化 (TLBO) 演算法基於課堂上教師與學習者之間的關係。在一個特定的課堂中，教師透過其辛勤工作向學生傳授知識。然後，學生或學習者彼此互動並提高他們的知識。

讓我們透過本文進一步瞭解基於教學學習的最佳化。

什麼是 TLBO？

讓我們考慮一個群體 p（特別是課堂）和課堂中學習者的數量 l。對於最佳化問題，可能存在決定性變數（學習者從中獲取知識的科目）。可以發生兩種學習模式：

• 透過教師（教學階段）

• 透過學習者之間相互互動（學習階段）

我們關注學習者的結果，這將是適應度值。

TLBO 最佳化函式

最佳化演算法涉及兩種型別的函式。它們是

• 球面函式 - 用於評估效能

其數學表示式為：

$$\mathrm{f(x_{1,}x_{2},.........x_{n})=\sum ^{n}_{i=0} \:\:x^{2}_{i}}$$

在 f(0,..0) = 0 處取得最小值

• Rastrigin 函式 - 用作測試函式的非凸函式，其數學表示式為：

$$\mathrm{f(x_{1,}x_{2},.........x_{n})=10+}\mathrm{\sum_{i=1}^{n} (x^{2}_{i}-10\cos\:\:\cos(2\prod x_{i})}$$

在 Python 中實現 TLBO 演算法

示例

import numpy as np
from pyMetaheuristic.algorithm import teaching_learning_based_optimization
from pyMetaheuristic.utils import graphs

def eas_opt(varval = [0, 0]):
   x_1, x_2 = varval
   fval = -np.cos(x_1) * np.cos(x_2) * np.exp(-(x_1 - np.pi) ** 2 - (x_2 - np.pi) ** 2)
   return fval
plt_params = {
   'min_values': (-6, -6),
   'max_values': (6, 6),
   'step': (0.2, 0.2),
   'solution': [],
   'proj_view': '3D',
   'view': 'notebook'
}
graphs.plot_single_function(target_function = eas_opt, **plt_params)

params = {
   'population_size': 15,
   'min_values': (-5, -5),
   'max_values': (5, 5),
   'generations': 500,
   'verbose': True
}
tlbo = teaching_learning_based_optimization(target_function = eas_opt, **params)

vars = tlbo[:-1]
min = tlbo[ -1]
print('Variables: ', np.around(vars, 5) , ' Minimum Value Found: ', round(min, 5) )

plt_params = {
   'min_values': (-6, -6),
   'max_values': (6, 6),
   'step': (0.2, 0.2),
   'solution': [vars],
   'proj_view': '3D',
   'view': 'notebook'
}
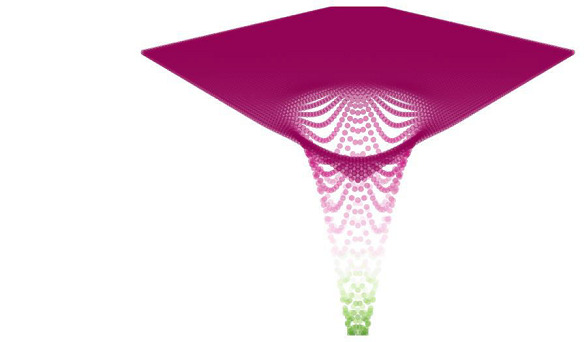
graphs.plot_single_function(target_function = eas_opt, **plt_params)

輸出

Generation = 0 f(x) = -0.5748727344288006
Generation = 1 f(x) = -0.7555913129284719
Generation = 2 f(x) = -0.9219320357862593
Generation = 3 f(x) = -0.9644524112155972
Generation = 4 f(x) = -0.9809361915349301
Generation = 5 f(x) = -0.991863434885587
Generation = 6 f(x) = -0.9984949247685845
Generation = 7 f(x) = -0.9991563851570532
Generation = 8 f(x) = -0.9997584334443873
Generation = 9 f(x) = -0.9997584334443873
Generation = 10 f(x) = -0.9998450580252695
Generation = 11 f(x) = -0.9998982502404465
Generation = 12 f(x) = -0.999961847330126
Generation = 13 f(x) = -0.9999810734164969
Generation = 14 f(x) = -0.9999930426674921
Generation = 15 f(x) = -0.9999995055655798
Generation = 16 f(x) = -0.9999999410594664
Generation = 17 f(x) = -0.9999999410594664
Generation = 18 f(x) = -0.9999999877205884
Generation = 19 f(x) = -0.9999999877205884
Generation = 20 f(x) = -0.9999999931826284
-------------------------------------------------------------
-------------------------------------------------------
Generation = 500 f(x) = -0.9999999991966855
Variables: [3.14161 3.14158] Minimum Value Found: -1.0

基於教學學習最佳化的優勢

• TLBO 演算法除了群體大小和迭代次數這兩個引數外，不需要任何其他引數即可執行。

• 它更準確，並且不需要導數。

• 遵循完整的路徑生成解決方案

基於教學學習最佳化的缺點

• 這是一個耗時的演算法

• 最佳化演算法執行需要大量的空間

結論

基於教學學習最佳化是一種基於群體的演算法，它嚴重依賴於教師與學習者之間以及學習者之間的學習關係。