資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究使用PyTorch進行手寫數字識別？
在本教程中，我們將使用PyTorch訓練一個卷積神經網路 (CNN) 來識別使用MNIST資料集的手寫數字。
MNIST是一個廣泛用於手寫數字分類任務的資料集，包含超過7萬張標記的28*28畫素灰度手寫數字影像。該資料集包含近6萬張訓練影像和1萬張測試影像。我們的任務是使用6萬張訓練影像訓練模型，然後在1萬張測試影像上測試其分類準確率。
安裝
首先，我們需要最新版本的MXNet，只需在終端執行以下命令：
$pip install mxnet
你將會看到類似於……的結果。
Collecting mxnet Downloading https://files.pythonhosted.org/packages/60/6f/071f9ef51467f9f6cd35d1ad87156a29314033bbf78ad862a338b9eaf2e6/mxnet-1.2.0-py2.py3-none-win32.whl (12.8MB) 100% |████████████████████████████████| 12.8MB 131kB/s Requirement already satisfied: numpy in c:\python\python361\lib\site-packages (from mxnet) (1.16.0) Collecting graphviz (from mxnet) Downloading https://files.pythonhosted.org/packages/1f/e2/ef2581b5b86625657afd32030f90cf2717456c1d2b711ba074bf007c0f1a/graphviz-0.10.1-py2.py3-none-any.whl …. …. Installing collected packages: graphviz, mxnet Successfully installed graphviz-0.10.1 mxnet-1.2.0
其次，我們需要torch和torchvision庫——如果你的環境中沒有，可以使用pip安裝。
匯入庫
import torch import torchvision
載入MNIST資料集
在開始編寫程式之前，我們需要MNIST資料集。因此，讓我們將影像和標籤載入到記憶體中，並定義我們將在此實驗中使用的超引數。
#n_epochs are the number of times, we'll loop over the complete training dataset n_epochs = 3 batch_size_train = 64 batch_size_test = 1000 #Learning_rate and momentum are for the opimizer learning_rate = 0.01 momentum = 0.5 log_interval = 10 random_seed = 1 torch.backends.cudnn.enabled = False torch.manual_seed(random_seed) <torch._C.Generator at 0x2048010c690>
現在我們將使用TorchVision載入MNIST資料集。我們使用批大小為64進行訓練，在該資料集上測試大小為1000。對於歸一化，我們將使用MNIST資料集的均值0.1307和標準差0.3081。
train_loader = torch.utils.data.DataLoader(
torchvision.datasets.MNIST('/files/', train=True, download=True,
transform=torchvision.transforms.Compose([
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize(
(0.1307,), (0.3081,))
])
),
batch_size=batch_size_train, shuffle=True)
test_loader = torch.utils.data.DataLoader(
torchvision.datasets.MNIST('/files/', train=False, download=True,
transform=torchvision.transforms.Compose([
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize(
(0.1307,), (0.3081,))
])
),
batch_size=batch_size_test, shuffle=True)輸出
Downloading http://yann.lecun.com/exdb/mnist/train-images-idx3-ubyte.gz Downloading http://yann.lecun.com/exdb/mnist/train-labels-idx1-ubyte.gz Downloading http://yann.lecun.com/exdb/mnist/t10k-images-idx3-ubyte.gz Downloading http://yann.lecun.com/exdb/mnist/t10k-labels-idx1-ubyte.gz Processing... Done!
使用test_loader載入測試資料
examples = enumerate(test_loader) batch_idx, (example_data, example_targets) = next(examples) example_data.shape
輸出
torch.Size([1000, 1, 28, 28])
從輸出中我們可以看到，一個測試資料批次是一個形狀為[1000, 1, 28, 28]的張量，這意味著1000個28*28畫素的灰度影像示例。
讓我們使用matplotlib繪製一些資料集。
import matplotlib.pyplot as plt
fig = plt.figure()
for i in range(5):
plt.subplot(2,3,i+1)
plt.tight_layout()
plt.imshow(example_data[i][0], cmap='gray', interpolation='none')
plt.title("Ground Truth: {}".format(example_targets[i]))
plt.xticks([])
plt.yticks([])
print(fig)輸出
構建網路
現在我們將使用兩個二維卷積層，然後是兩個全連線層來構建我們的網路。我們將為我們想要構建的網路建立一個新類，但在那之前，讓我們匯入一些模組。
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(1, 10, kernel_size=5)
self.conv2 = nn.Conv2d(10, 20, kernel_size=5)
self.conv2_drop = nn.Dropout2d()
self.fc1 = nn.Linear(320, 50)
self.fc2 = nn.Linear(50, 10)
def forward(self, x):
x = F.relu(F.max_pool2d(self.conv1(x), 2))
x = F.relu(F.max_pool2d(self.conv2_drop(self.conv2(x)), 2))
x = x.view(-1, 320)
x = F.relu(self.fc1(x))
x = F.dropout(x, training=self.training)
x = self.fc2(x)
return F.log_softmax(x)初始化網路和最佳化器
network = Net() optimizer = optim.SGD(network.parameters(), lr = learning_rate,momentum = momentum)
訓練模型
讓我們構建我們的訓練模型。首先檢查我們的網路是否處於網路模式，然後在每個epoch中迭代所有訓練資料一次。資料載入器將載入單個批次。我們使用optimizer.zero_grad()將梯度設定為零。
train_losses = [] train_counter = [] test_losses = [] test_counter = [i*len(train_loader.dataset) for i in range(n_epochs + 1)]
為了建立一個漂亮的訓練曲線，我們建立兩個列表來儲存訓練和測試損失。在x軸上，我們想顯示訓練樣本的數量。
透過backward()呼叫，我們現在收集一組新的梯度，我們使用optimizer.step()將其反向傳播到網路的每個引數中。
def train(epoch):
network.train()
for batch_idx, (data, target) in enumerate(train_loader):
optimizer.zero_grad()
output = network(data)
loss = F.nll_loss(output, target)
loss.backward()
optimizer.step()
if batch_idx % log_interval == 0:
print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
epoch, batch_idx * len(data), len(train_loader.dataset),
100. * batch_idx / len(train_loader), loss.item()))
train_losses.append(loss.item())
train_counter.append(
(batch_idx*64) + ((epoch-1)*len(train_loader.dataset)))
torch.save(network.state_dict(), '/results/model.pth')
torch.save(optimizer.state_dict(), '/results/optimizer.pth')神經網路模組以及最佳化器都能夠使用.state_dict()儲存和載入其內部狀態。
現在對於我們的測試迴圈，我們總結測試損失並跟蹤正確分類的數字以計算網路的準確率。
def test():
network.eval()
test_loss = 0
correct = 0
with torch.no_grad():
for data, target in test_loader:
output = network(data)
test_loss += F.nll_loss(output, target, size_average=False).item()
pred = output.data.max(1, keepdim=True)[1]
correct += pred.eq(target.data.view_as(pred)).sum()
test_loss /= len(test_loader.dataset)
test_losses.append(test_loss)
print('\nTest set: Avg. loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
test_loss, correct, len(test_loader.dataset),
100. * correct / len(test_loader.dataset)))為了執行訓練，我們在遍歷n_epochs之前新增一個test()呼叫，以使用隨機初始化的引數評估我們的模型。
test() for epoch in range(1, n_epochs + 1): train(epoch) test()
輸出
Test set: Avg. loss: 2.3048, Accuracy: 1063/10000 (10%) Train Epoch: 1 [0/60000 (0%)]Loss: 2.294911 Train Epoch: 1 [640/60000 (1%)]Loss: 2.314225 Train Epoch: 1 [1280/60000 (2%)]Loss: 2.290719 Train Epoch: 1 [1920/60000 (3%)]Loss: 2.294191 Train Epoch: 1 [2560/60000 (4%)]Loss: 2.246799 Train Epoch: 1 [3200/60000 (5%)]Loss: 2.292224 Train Epoch: 1 [3840/60000 (6%)]Loss: 2.216632 Train Epoch: 1 [4480/60000 (7%)]Loss: 2.259646 Train Epoch: 1 [5120/60000 (9%)]Loss: 2.244781 Train Epoch: 1 [5760/60000 (10%)]Loss: 2.245569 Train Epoch: 1 [6400/60000 (11%)]Loss: 2.203358 Train Epoch: 1 [7040/60000 (12%)]Loss: 2.192290 Train Epoch: 1 [7680/60000 (13%)]Loss: 2.040502 Train Epoch: 1 [8320/60000 (14%)]Loss: 2.102528 Train Epoch: 1 [8960/60000 (15%)]Loss: 1.944297 Train Epoch: 1 [9600/60000 (16%)]Loss: 1.886444 Train Epoch: 1 [10240/60000 (17%)]Loss: 1.801920 Train Epoch: 1 [10880/60000 (18%)]Loss: 1.421267 Train Epoch: 1 [11520/60000 (19%)]Loss: 1.491448 Train Epoch: 1 [12160/60000 (20%)]Loss: 1.600088 Train Epoch: 1 [12800/60000 (21%)]Loss: 1.218677 Train Epoch: 1 [13440/60000 (22%)]Loss: 1.060651 Train Epoch: 1 [14080/60000 (23%)]Loss: 1.161512 Train Epoch: 1 [14720/60000 (25%)]Loss: 1.351181 Train Epoch: 1 [15360/60000 (26%)]Loss: 1.012257 Train Epoch: 1 [16000/60000 (27%)]Loss: 1.018847 Train Epoch: 1 [16640/60000 (28%)]Loss: 0.944324 Train Epoch: 1 [17280/60000 (29%)]Loss: 0.929246 Train Epoch: 1 [17920/60000 (30%)]Loss: 0.903336 Train Epoch: 1 [18560/60000 (31%)]Loss: 1.243159 Train Epoch: 1 [19200/60000 (32%)]Loss: 0.696106 Train Epoch: 1 [19840/60000 (33%)]Loss: 0.902251 Train Epoch: 1 [20480/60000 (34%)]Loss: 0.986816 Train Epoch: 1 [21120/60000 (35%)]Loss: 1.203934 Train Epoch: 1 [21760/60000 (36%)]Loss: 0.682855 Train Epoch: 1 [22400/60000 (37%)]Loss: 0.653592 Train Epoch: 1 [23040/60000 (38%)]Loss: 0.932158 Train Epoch: 1 [23680/60000 (39%)]Loss: 1.110188 Train Epoch: 1 [24320/60000 (41%)]Loss: 0.817414 Train Epoch: 1 [24960/60000 (42%)]Loss: 0.584215 Train Epoch: 1 [25600/60000 (43%)]Loss: 0.724121 Train Epoch: 1 [26240/60000 (44%)]Loss: 0.707071 Train Epoch: 1 [26880/60000 (45%)]Loss: 0.574117 Train Epoch: 1 [27520/60000 (46%)]Loss: 0.652862 Train Epoch: 1 [28160/60000 (47%)]Loss: 0.654354 Train Epoch: 1 [28800/60000 (48%)]Loss: 0.811647 Train Epoch: 1 [29440/60000 (49%)]Loss: 0.536885 Train Epoch: 1 [30080/60000 (50%)]Loss: 0.849961 Train Epoch: 1 [30720/60000 (51%)]Loss: 0.844555 Train Epoch: 1 [31360/60000 (52%)]Loss: 0.687859 Train Epoch: 1 [32000/60000 (53%)]Loss: 0.766818 Train Epoch: 1 [32640/60000 (54%)]Loss: 0.597061 Train Epoch: 1 [33280/60000 (55%)]Loss: 0.691049 Train Epoch: 1 [33920/60000 (57%)]Loss: 0.573049 Train Epoch: 1 [34560/60000 (58%)]Loss: 0.405698 Train Epoch: 1 [35200/60000 (59%)]Loss: 0.480660 Train Epoch: 1 [35840/60000 (60%)]Loss: 0.582871 Train Epoch: 1 [36480/60000 (61%)]Loss: 0.496494 …… …… ……. Train Epoch: 3 [49920/60000 (83%)]Loss: 0.253500 Train Epoch: 3 [50560/60000 (84%)]Loss: 0.364354 Train Epoch: 3 [51200/60000 (85%)]Loss: 0.333843 Train Epoch: 3 [51840/60000 (86%)]Loss: 0.096922 Train Epoch: 3 [52480/60000 (87%)]Loss: 0.282102 Train Epoch: 3 [53120/60000 (88%)]Loss: 0.236428 Train Epoch: 3 [53760/60000 (90%)]Loss: 0.610584 Train Epoch: 3 [54400/60000 (91%)]Loss: 0.198840 Train Epoch: 3 [55040/60000 (92%)]Loss: 0.344225 Train Epoch: 3 [55680/60000 (93%)]Loss: 0.158644 Train Epoch: 3 [56320/60000 (94%)]Loss: 0.216912 Train Epoch: 3 [56960/60000 (95%)]Loss: 0.309554 Train Epoch: 3 [57600/60000 (96%)]Loss: 0.243239 Train Epoch: 3 [58240/60000 (97%)]Loss: 0.176541 Train Epoch: 3 [58880/60000 (98%)]Loss: 0.456749 Train Epoch: 3 [59520/60000 (99%)]Loss: 0.318569 Test set: Avg. loss: 0.0912, Accuracy: 9716/10000 (97%)
評估模型的效能
因此，僅經過3個epoch的訓練，我們就達到了97%的測試集準確率。在開始訓練之前，我們使用隨機初始化的引數，測試集的初始準確率為10%。
讓我們繪製我們的訓練曲線
fig = plt.figure()
plt.plot(train_counter, train_losses, color='blue')
plt.scatter(test_counter, test_losses, color='red')
plt.legend(['Train Loss', 'Test Loss'], loc='upper right')
plt.xlabel('number of training examples seen')
plt.ylabel('negative log likelihood loss')
fig輸出
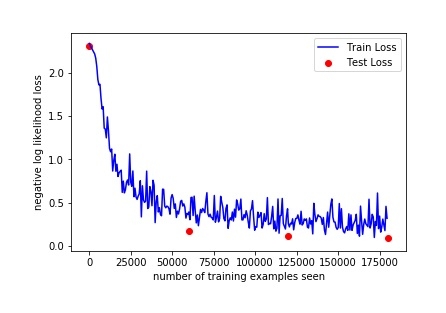
透過檢查上面的輸出，我們可以增加epoch的數量以檢視更多結果，因為透過檢查3個epoch可以提高準確率。
但在那之前，執行一些更多示例並比較模型的輸出
with torch.no_grad():
output = network(example_data)
fig = plt.figure()
for i in range(6):
plt.subplot(2,3,i+1)
plt.tight_layout()
plt.imshow(example_data[i][0], cmap='gray', interpolation='none')
plt.title("Prediction: {}".format(
output.data.max(1, keepdim=True)[1][i].item()))
plt.xticks([])
plt.yticks([])
fig
正如我們可以看到我們的模型預測，對於這些示例，它看起來非常準確。
更新於：2019年7月30日
瀏覽量：232
廣告