資料結構
網路
RDBMS
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究如何將帶有 ε 的 NFA 轉換為 DFA？（理論計算機科學）
在這個方法中，我們首先將帶有 ε 的非確定性有限自動機 (NFA) 轉換為不帶 ε 的 NFA。
然後，不帶 ε 的 NFA 可以轉換為其等效的確定性有限自動機 (DFA)。
轉換方法
將帶有 ε 的 NFA 轉換為 DFA 的方法解釋如下：
步驟 1 - 假設 M={Q, Σ, δ,q0,F) 是帶有 ε 的 NFA。我們必須將這個帶有 ε 的 NFA 轉換為等效的 DFA，記為
M0=(Q0,Σ, δ0,q0,F0)
然後得到：
ε-閉包(q0) ={p1,p2,p3,……pn}
然後 [p1,p2,p2,….pn] 成為 DFA 的起始狀態
現在 [p1,p2,p3,….pn] ∈ Q0
步驟 2 - 我們將為每個輸入獲得 [p1,p2,p3,…pn] 上的 δ 轉移。
δ 0([p1,p2,p3,..pn],a) = ε-閉包(δ(p1,a) U δ(p2,a2)U……………… δ(pn,a))
= U (i=1 to n) ε-閉包 d(pi,a)
其中 a 是輸入 ∈Σ
步驟 3 - 獲得的狀態 [p1,p2,p3,…pn] ∈ Q0。
包含最終狀態 pi 的狀態是 DFA 中的最終狀態
示例
將以下帶有 epsilon 的 NFA 轉換為等效的 DFA
解答
考慮以下用於將帶有 epsilon 的 NFA 轉換為 DFA 的 NFA：
為了轉換這個帶有 epsilon 的 NFA，我們將首先找到 ε-閉包，如下所示：
- ε-閉包(q0)={q0,q1,q2}
- ε-閉包(q1)={q1,q2}
- ε-閉包(q2)={q2}
讓我們從起始狀態的 ε-閉包開始，如下所示：
當 ε-閉包(q0)={q0,q1,q2} 時，我們將此狀態稱為 A。
現在，讓我們找到對 A 的每個輸入符號的轉移，如下所示：
δ'(A, a) = ε-closure(δ(A,a))
= ε-closure(δ(q0,q1,q2), a))
= ε-closure(δ(q0, a) ∪ δ(q1,a) U δ(q2,a) )
= ε-closure(ΦUq1 ∪q2)
= ε-closure(q1)
= {q1, q2} let us call it as state B
δ'(A, b) = ε-closure(δ(A,b))
= ε-closure(δ(q0,q1,q2), b))
= ε-closure(δ(q0, b) ∪ δ(q1,b) U δ(q2,b) )
= ε-closure(q0 U Φ∪q0)
= ε-closure(q0)
= {q0,q1, q2} its nothing but state A
δ'(B, a) = ε-closure(δ(B,a))
= ε-closure(δ(q1,q2), a))
= ε-closure(δ(q1,a) U δ(q2,a) )
= ε-closure(q1 ∪q2)
= ε-closure(q1)
= {q1, q2} its nothing but state B
δ'(B, b) = ε-closure(δ(B,b))
= ε-closure(δ(q1,q2), b))
= ε-closure(δ(q1,b) U δ(q2,b) )
= ε-closure(Φ∪q0)
= ε-closure(q0)
= {q0,q1, q2} its nothing but state A因此，生成的 DFA 的狀態轉換表如下：
| 狀態\輸入 | a | b |
|---|---|---|
| A | B | A |
| B | B | A |
DFA 圖如下所示：
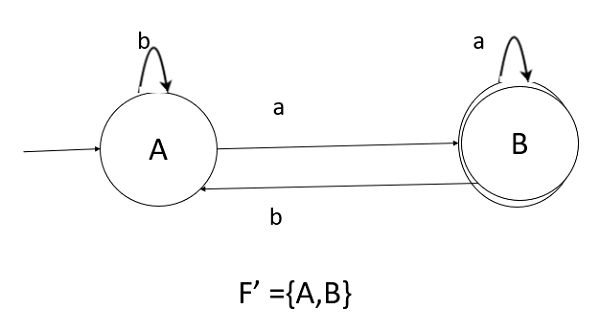
- 由於 A={q0,q1,q2} 中包含最終狀態 q2，因此 A 是最終狀態。
- 在 B ={q1,q2} 中包含狀態 q2。因此，B 也是最終狀態。
更新於：2023年9月13日
44K+ 次瀏覽
廣告