給出一個將 NFA 轉換為 DFA 的示例問題。
問題
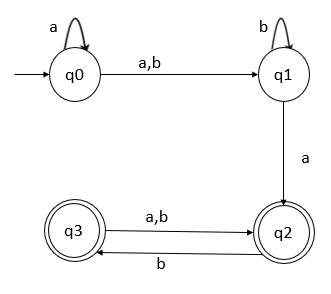
考慮一個非確定有限自動機 (NFA),並將該 NFA 轉換為等效確定有限自動機 (DFA)。
解決方案
讓我們為給定的圖表構建 NFA 轉換表 −
| 狀態\輸入 | a | b |
|---|---|---|
| ->q0 | {q0,q1} | q0 |
| q1 | q2 | q1 |
| q2 | q3 | q3 |
| q3 | - | q2 |
DFA 不能有多個狀態。因此,在上圖中將 {q0,q1} 視為一個狀態。
我們來將上面的表格轉換為等效的 DFA
| 狀態\輸入 | a | b |
|---|---|---|
| ->q1 | [q0,q1] | q0 |
| [q0,q1] | [q0q1q2] | [q0q1] |
| *[q0q1q2] | [q0q1q2q3] | [q0q1q3] |
| *[q0q1q2q3] | [q0q1q2q3] | [q0q1q2q3] |
| *[q0q1q3] | [q0q1q2] | [q0q1q2] |
在 DFA 中,終態是 q2 和 q3,無論 q2 和 q3 出現於何處,該狀態都變為終態。
現在,DFA 的轉換圖如下 −
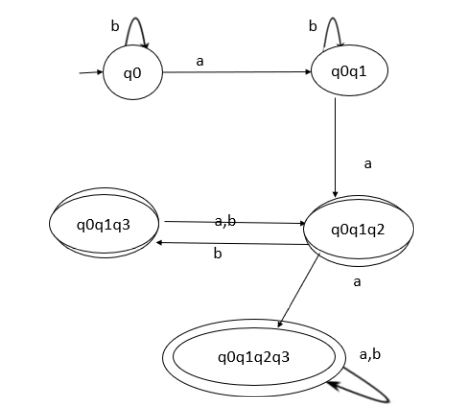

廣告

 資料結構
資料結構 網路
網路 RDBMS
RDBMS 作業系統
作業系統 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 程式設計
C 程式設計 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP